
【題目】已知直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與直線
,與直線![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,直線
,直線![]() 與
與![]() 軸正半軸、
軸正半軸、![]() 軸圍成的
軸圍成的![]() 的面積為
的面積為![]() .
.
(1)求直線![]() 的解析式;
的解析式;
(2)求點(diǎn)![]() 坐標(biāo)并判斷
坐標(biāo)并判斷![]() 的形狀,說明理由;
的形狀,說明理由;
(3)在![]() 軸上找一點(diǎn)
軸上找一點(diǎn)![]() ,使
,使![]() 的面積為
的面積為![]() ,求
,求![]() 點(diǎn)坐標(biāo).
點(diǎn)坐標(biāo).
【答案】(1)![]() ;(2)
;(2)![]() ;直角三角形;(3)
;直角三角形;(3)![]() 或
或![]()
【解析】
(1)根據(jù)待定系數(shù)法即可求得;
(2)根據(jù)△BOC的面積求得C的坐標(biāo),然后根據(jù)勾股定理求得AC,AB、BC的長,根據(jù)勾股定理的逆定理即可判定△ABC是直角三角形;
(3)設(shè)P(x,0),則AP=|x+4|,根據(jù)三角形面積公式即可得到![]() ,解得即可.
,解得即可.
(1)設(shè)直線l1的解析式為y=kx+b,
∵直線l1,與x軸交于點(diǎn)A(-4,0),與直線l2相交于點(diǎn)B(0,3)
∴![]()
解得![]()
∴直線l1的解析式為![]()
故答案為:![]()
(2)設(shè)C(m,0),![]() ,
,
∵△BOC的面積為![]()
∴![]()
即![]()
解得m=![]()
∴C(![]() ,0),
,0),
∴AC=4+![]() =
=![]()
則AC2=![]()
∵AB2=32+42=25,BC2=(![]() )2+32=
)2+32=![]()
∴AB2+BC2=25+![]() =
=![]()
∴AB2+BC2=AC2,
∴△ABC是直角三角形;
故答案為:直角三角形,理由見解析
(3)設(shè)P(x,0),則AP=|x+4|,
∵△BAP的面積為9,![]() APOB=9,即
APOB=9,即
![]() |x-4|×3=9,
|x-4|×3=9,
解得x1=2,x2=-10,
∴P點(diǎn)的坐標(biāo)為(2,0)或(-10,0)
故答案為: (2,0)或(-10,0)



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,且拋物線經(jīng)過A(1,0),C(0,3)兩點(diǎn),與x軸交于點(diǎn)B.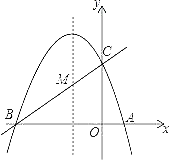
(1)若直線y=mx+n經(jīng)過B、C兩點(diǎn),求直線BC和拋物線的解析式;
(2)在拋物線的對稱軸x=﹣1上找一點(diǎn)M,使點(diǎn)M到點(diǎn)A的距離與到點(diǎn)C的距離之和最小,求出點(diǎn)M的坐標(biāo);
(3)設(shè)點(diǎn)P為拋物線的對稱軸x=﹣1上的一個動點(diǎn),求使△BPC為直角三角形的點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,矩形OABC的頂點(diǎn)A、C分別在x軸的負(fù)半軸、y軸的正半軸上,點(diǎn)B在第二象限.將矩形OABC繞點(diǎn)O順時針旋轉(zhuǎn),使點(diǎn)B落在y軸上,得到矩形ODEF,BC與OD相交于點(diǎn)M.若經(jīng)過點(diǎn)M的反比例函數(shù)y= ![]() (x<0)的圖象交AB于點(diǎn)N,S矩形OABC=32,tan∠DOE=
(x<0)的圖象交AB于點(diǎn)N,S矩形OABC=32,tan∠DOE= ![]() ,則BN的長為 .
,則BN的長為 . 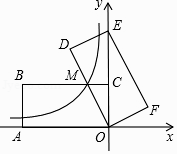
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=2,與x軸的一個交點(diǎn)坐標(biāo)為(4,0),其部分圖象如圖所示,下列結(jié)論:
①拋物線過原點(diǎn);
②4a+b+c=0;
③a﹣b+c<0;
④拋物線的頂點(diǎn)坐標(biāo)為(2,b);
⑤當(dāng)x<2時,y隨x增大而增大.
其中結(jié)論正確的是( )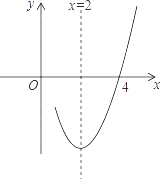
A.①②③
B.③④⑤
C.①②④
D.①④⑤
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線y=ax2+3與x軸的兩個交點(diǎn)分別為(m,0)和(n,0),則當(dāng)x=m+n時,y的值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】請把以下證明過程補(bǔ)充完整:
已知:如圖,∠A=∠F,∠C=∠D.點(diǎn)B,E分別在線段AC,DF上,對∠1=∠2進(jìn)行說理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(兩直線平行,內(nèi)錯角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代換)
∴______∥______(同位角相等,兩直線平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代換).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,高BD,CE交于點(diǎn)O,AO交BC于點(diǎn)F,則圖中共有全等三角形( )

A.8對B.7對C.6對D.5對
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,AB=12,點(diǎn)E在邊BC上,BE=EC,將△DCE沿DE對折至△DFE,延長EF交邊AB于點(diǎn)G,連接DG、BF,給出以下結(jié)論:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正確結(jié)論的個數(shù)是( )
.其中所有正確結(jié)論的個數(shù)是( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知x+ ![]() =3,則下列三個等式:①x2+
=3,則下列三個等式:①x2+ ![]() =7,②x﹣
=7,②x﹣ ![]() ,③2x2﹣6x=﹣2中,正確的個數(shù)有( )
,③2x2﹣6x=﹣2中,正確的個數(shù)有( )
A.0個
B.1個
C.2個
D.3個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com