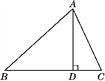
【題目】如圖，在△ABC中，AD是BC邊上的高，tanB＝cos∠DAC.
（1）求證：AC＝BD；
（2）若sin C＝
，BC＝12，求△ABC的面積．
【答案】（1）證明見解析；（2）△ABC的面積為48.
【解析】(1)∵AD是BC上的高，∴AD⊥BC．
∴∠ADB=90°，∠ADC=90°． …………………………………………1分
在Rt△ABD和Rt△ADC中，
∵
=
， 
=
…………………………………………3分
又已知
∴
=
．∴AC=BD． ………………………………4分
(2)在Rt△ADC中， 
，故可設AD=12k，AC=13k．
∴CD=
=5k．………………………………5分
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k ………………………………6分
由已知BC=12， ∴18k=12．∴k=
． ………………………………7分
∴AD=12k=12
=8． ……………………………8分
（1）在直角三角形中，表示
，根據它們相等，即可得出結論
（2）利用
和勾股定理表示出線段長，根據
，求出
長
科目：初中數學 來源： 題型：
【題目】如圖，把Rt△ABC放在直角坐標系內，其中∠CAB＝90°，BC＝5，點A，B的坐標分別為(1，0)，(4，0)，將△ABC沿x軸向右平移，當點C落在直線y＝2x－6上時，線段BC掃過的面積為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠BAC=90°，AD⊥BC，垂足為D，則下面的結論中正確的個數為（ ）
①AB與AC互相垂直；
②AD與AC互相垂直；
③點C到AB的垂線段是線段AB；
④線段AB的長度是點B到AC的距離；
⑤線段AB是B點到AC的距離．
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=AC，點D為BC上一點，且AD=DC，過A，B，D三點作⊙O，AE是⊙O的直徑，連結DE．
（1）求證：AC是⊙O的切線；
（2）若sinC=
，AC=6，求⊙O的直徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一項工程，甲隊單獨做需40天完成，若乙隊先做30天后，甲、乙兩隊一起合做20天恰好完成任務，請問：
（1）乙隊單獨做需要多少天才能完成任務？
（2）現將該工程分成兩部分，甲隊做其中一部分工程用了x天，乙隊做另一部分工程用了y天，若x; y都是正整數，且甲隊做的時間不到15天，乙隊做的時間不到70天，那么兩隊實際各做了多少天？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知 A（-4，0），B（0，2），C（0，-3），D（2，0）
（1）在圖 1 中，畫出四邊形 ABDC，直接寫出四邊形 ABDC 的面積是 .
（2）點 E 是直線 AB 和 CD 的交點，求△ACE 的面積.
（3）點 P 的坐標為（0，p），△PAB 的面積大于△PCD 的面積，求 p 的取值范圍.
圖 1 備用圖
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點A，C，D，E在Rt△MON的邊上，∠MON=90°，AE⊥AB且AE=AB，BC⊥CD且BC=CD，BH⊥ON于點H，DF⊥ON于點F，OM=12，OE=6，BH=3，DF=4，FN=8，圖中陰影部分的面積為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個批發商銷售成本為20元/千克的某產品，根據物價部門規定：該產品每千克售價不得超過90元，在銷售過程中發現的售量y（千克）與售價x（元/千克）滿足一次函數關系，對應關系如下表：
售價x（元/千克） | … | 50 | 60 | 70 | 80 | … |
銷售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y與x的函數關系式；
（2）該批發商若想獲得4000元的利潤，應將售價定為多少元？
（3）該產品每千克售價為多少元時，批發商獲得的利潤w（元）最大？此時的最大利潤為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
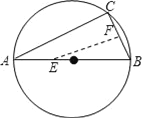
【題目】如圖，AB是⊙O的直徑，弦BC=2cm，F是弦BC的中點，∠ABC=60°．若動點E以2cm/s的速度從A點出發沿著ABA方向運動，設運動時間為t（s）（0≤t＜3），連接EF，當t為_____s時，△BEF是直角三角形．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com