【題目】一只箱子里共有3個球，其中2個白球，1個紅球，它們除顏色外圴相同．
（1）從箱子里任意摸出一個球是白球的概率是多少？
（2）從箱子里任意摸出一個球，不將它放回，攪均后再摸出一球，求兩次摸出的球都是白球的概率，并畫出樹狀圖．
【答案】
（1）解：從箱子中任意摸出一個球是白球的概率是 
（2）解：記兩個白球分別為白1與白2，畫樹狀圖如右所示：
從樹狀圖可看出：事件發生的所有可能的結果總數為6，兩次摸出球的都是白球的結果總數為2，因此其概率 
．
【解析】（1）由題意可知一共有3個球，白球有2個，根據概率公式即可求出任意摸出一個球是白球的概率。
（2）根據從箱子里任意摸出一個球，不將它放回，攪均后再摸出一球，列出樹狀圖，再求出所有等可能的結果數及兩次摸出的球都是白球的可能數，根據概率公式即可求出兩次摸出的球都是白球的概率。
【考點精析】本題主要考查了列表法與樹狀圖法和概率公式的相關知識點，需要掌握當一次試驗要設計三個或更多的因素時，用列表法就不方便了，為了不重不漏地列出所有可能的結果，通常采用樹狀圖法求概率；一般地，如果在一次試驗中，有n種可能的結果，并且它們發生的可能性都相等，事件A包含其中的m中結果，那么事件A發生的概率為P（A）=m/n才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】已知關于 
的一元二次方程 x2+（2m-1）x+m2=0有兩個實數根 x1 和 x2 ．
（1）求實數 m 的取值范圍；
（2）當 x12-x22 時，求 m 的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
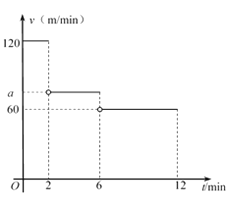
【題目】小明從家出發，沿一條直道散步到離家450 m的郵局，經過一段時間原路返回，剛好在第12 min回到家中．設小明出發第t min時的速度為v m/min，v與t之間的函數關系如圖所示(圖中的空心圈表示不包含這一點)．
(1)小明出發第2 min時離家的距離為 m；
(2)當2＜ t ≤6時，求小明的速度a；
(3)求小明到達郵局的時間．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲組的
名工人12月份完成的總工作量比此月人均定額的
倍多
件，乙組的名工人12月份完成的總工作量比此月人均定額的
倍少件.
（1）如果兩組工人實際完成的此月人均工作量相等，那么此月的人均定額是多少件？
（2）如果甲組工人實際完成的此月人均工作量比乙組工人實際完成的此月人均工作量少3件，那么此月人均定額是多少件？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2012年6月1日起，國家實施了中央財政補貼條例支持高效節能電器的推廣使用，某款定速空調在條例實施后，每購買一臺，客戶可獲財政補貼200元，若同樣用11萬元所購買的此款空調數臺，條例實施后比實施前多10%．求條例實施前此款空調的單價．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，O為直線AB上一點，∠COE=90°,OF平分∠AOE.
（1）若∠COF=40°，求∠BOE的度數.
（2）若∠COF=α（0°＜α＜90°），則∠BOE=______（用含α的式子表示）.
查看答案和解析>>
科目：初中數學 來源： 題型：
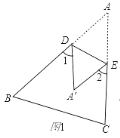
【題目】(1)如圖1，把△ABC沿DE折疊，使點A落在點A’處，試探索∠1+∠2與∠A的關系．（證明）．
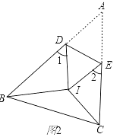
(2)如圖2，BI平分∠ABC，CI平分∠ACB，把△ABC折疊，使點A與點I重合，若∠1+∠2=130°，求∠BIC的度數；
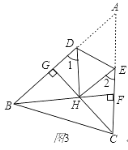
(3)如圖3，在銳角△ABC中，BF⊥AC于點F，CG⊥AB于點G，BF、CG交于點H，把△ABC折疊使點A和點H重合，試探索∠BHC與∠1+∠2的關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，以平行四邊形ABCD的頂點A為圓心，AB為半徑作圓，分別交BC，AD于E，F兩點，交BA的延長于G，判斷弧EF和弧FG是否相等，并說明理由。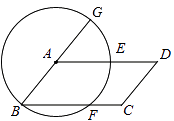
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
