【題目】如圖，已知A（3，1），B（1，0），PQ是直線y=x上的一條動線段且PQ=
（Q在P的下方），當AP+PQ+QB取最小值時，點Q坐標為______．
【答案】（
，）
【解析】
作點B關于直線y=x的對稱點B'（0，1），過點A作直線MN∥PQ，并沿MN把點A向下平移
單位后得A'（2，0），連接A'B'交直線y=x于點Q，求出直線A'B'解析式，與y=x組成方程組，可求Q點坐標．
解：作點B關于直線y=x的對稱點B'（0，1），過點A作直線MN∥PQ，并沿MN把點A向下平移單位后得A'（2，0），連接A'B'交直線y=x于點Q，如圖，
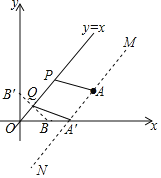
∵AA'=PQ=，AA'∥PQ，
∴四邊形APQA'是平行四邊形．
∴AP=A'Q．
∵AP+PQ+QB=B'Q+A'Q+PQ且PQ=．
∴當A'Q+B'Q值最小時，AP+PQ+QB值最小．
根據兩點之間線段最短，即A'，Q，B'三點共線時A'Q+B'Q值最小．
∵B'（0，1），A'（2，0），
∴直線A'B'的解析式y=-
x+1．
∴x=-x+1．即x=，
∴Q點坐標（，）．
故答案是：（，）．
名校課堂系列答案科目：初中數學 來源： 題型：
【題目】已知一次函數y＝﹣
x+2的圖象，繞x軸上一點P（m，0）旋轉180°，所得的圖象經過（0．﹣1），則m的值為（ ）
A.﹣2B.﹣1C.1D.2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(12分)如圖，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于點D.點P從點D出發，沿線段DC向點C運動，點Q從點C出發，沿線段CA向點A運動，兩點同時出發，速度都為每秒1個單位長度，當點P運動到C時，兩點都停止．設運動時間為t秒．
(1)求線段CD的長；
(2)設△CPQ的面積為S，求S與t之間的函數關系式，并確定在運動過程中是否存在某一時刻t，使得S△CPQ∶S△ABC＝9∶100？若存在，求出t的值；若不存在，說明理由；
(3)當t為何值時，△CPQ為等腰三角形？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖．在Rt△ABC中，∠ABC=90°，點D是斜邊上的中點，點P在AB上，PE⊥BD于E，PF⊥AC于F，若AB=6，BC=3，則PE+PF=（ ）
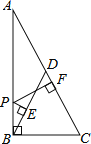
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，在矩形ABCD中，AC是對角線，點P為矩形外一點且滿足AP=PC，AP⊥PC，PC交AD于點N，連接DP，過點P作PM⊥PD交AD于M．
（1）若AP=5，AB=
BC，求矩形ABCD的面積；
（2）若CD=PM，試判斷線段AC、AP、PN之間的關系，并證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為配合全市“禁止焚燒秸稈”工作，某學校舉行了“禁止焚燒秸稈，保護環境，從我做起”為主題的演講比賽. 賽后組委會整理參賽同學的成績，并制作了如下不完整的頻數分布表和頻數分布直方圖，請根據圖表提供的信息，解答下列問題：
分數段 （分數為x分） | 頻數 | 百分比 |
60≤x＜70 | 8 | 20% |
70≤x＜80 | a | 30% |
80≤x＜90 | 16 | b% |
90≤x＜100 | 4 | 10% |
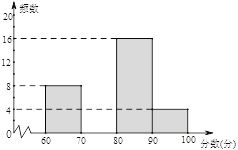
（1）表中的a＝ ，b＝ ；
（2）請補全頻數分布直方圖；
（3）若用扇形統計圖來描述成績分布情況，則分數段70≤x＜80對應的圓心角的度數是 ；
（4）競賽成績不低于90分的4名同學中正好有2名男同學，2名女同學.學校從這4名同學中隨機抽取2名同學接受電視臺記者采訪，請用列表或畫樹狀圖的方法求正好抽到一名男同學和一名女同學的概率.
查看答案和解析>>
科目：初中數學 來源： 題型：
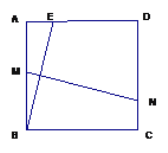
【題目】如圖，在正方形ABCD中，AB=
，E是AD邊上的一點(點E與點A和點D不重合)，BE的垂直平分線交AB于點M，交DC于點N.
(1)證明：MN = BE.
(2)設AE=
，四邊形ADNM的面積為S，寫出S關于的函數關系式.
(3)當AE為何值時，四邊形ADNM的面積最大？最大值是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
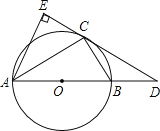
【題目】如圖，已知⊙O是△ABC的外接圓，AB是⊙O的直徑，點D是AB延長線上的一點，AE⊥DC交DC的延長線于點E，AC平分∠DAE．
（1）DE與⊙O有何位置關系？請說明理由．
（2）若AB=6，CD=4，求CE的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
