
【題目】(1)閱讀下面的材料并把解答過程補充完整.
問題:在關于![]() ,
,![]() 的二元一次方程組
的二元一次方程組![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
在關于![]() ,
,![]() 的二元一次方程組中,利用參數
的二元一次方程組中,利用參數![]() 的代數式表示
的代數式表示![]() ,
,![]() ,然后根據
,然后根據![]() ,
,![]() 列出關于參數
列出關于參數![]() 的不等式組即可求得
的不等式組即可求得![]() 的取值范圍.解:由
的取值范圍.解:由![]() ,解得
,解得 ,又因為
,又因為![]() ,
,![]() ,所以
,所以 解得____________.
解得____________.
(2)請你按照上述方法,完成下列問題:
①已知![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
②已知![]() ,在關于
,在關于![]() ,
,![]() 的二元一次方程組
的二元一次方程組![]() 中,
中,![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 的取值范圍(結果用含
的取值范圍(結果用含![]() 的式子表示)____________.
的式子表示)____________.
【答案】(1)0<a<2;(2)①2<x+y<6;②3m<a+b<4m.
【解析】
(1)先求出不等式組中每一個不等式的解集,再求出它們的公共部分即可;
(2)①根據(1)閱讀中的方法解題即可求解;
②解方程組![]() 得:
得:![]() ,根據x<0,y>0可得1.5<a<2,進一步得到a+b的取值范圍.
,根據x<0,y>0可得1.5<a<2,進一步得到a+b的取值范圍.
(1) 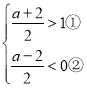 ,
,
∵解不等式①得:a>0,
解不等式②得:a<2,
∴不等式組的解集為0<a<2,
故答案為:0<a<2;
(2)①設x+y=a,則![]() ,
,
解得: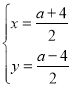 ,
,
∵x>3,y<1,
∴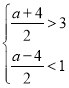 ,
,
解得:2<a<6,
即2<x+y<6;
②解方程組![]() 得:
得:![]() ,
,
∵x<0,y>0,
∴![]() ,
,
解得:1.5<a<2,
∵ab=m,
3m<a+b<4m.
故答案為:3m<a+b<4m.


 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD的形外分別作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
連結AC、EF.在圖中找一個與△FAE全等的三角形,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O與Rt△ABC的斜邊AB相切于點D,與直角邊AC相交于E,F兩點,連結DE,已知∠B=30°,⊙O的半徑為6,弧DE的長度為2π.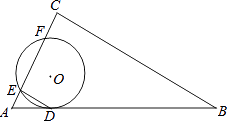
(1)求證:DE∥BC;
(2)若AF=CE,求線段BC的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
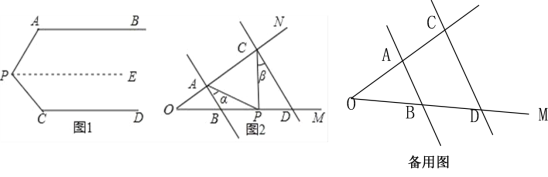
【題目】問題情境:如圖1,AB∥CD,∠PAB=125°,∠PCD=135°,求∠APC的度數.
小明的思路是:過P作PE∥AB,通過平行線性質來求∠APC.
(1)按小明的思路,易求得∠APC的度數為 度。
(2)問題遷移:如圖2,AB∥CD,點P在射線OM上運動,記∠PAB=α,∠PCD=β,當點P在B、D兩點之間運動時,問∠APC與α、β之間有何數量關系?請說明理由;
(3)在(2)的條件下,①如果點P運動到D點右側(不包括D點),則∠APC與α、β之間的數量關系為 .②如果點P運動到B點左側(不包括B點),則∠APC與α、β之間的數量關系 .(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等,經洽談,甲商場優惠方案是:每購買十套隊服,送一個足球;乙商場優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)求每套隊服和每個足球的價格是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用;
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園安全”受到全社會的廣泛關注,某校政教處對部分學生及家長就校園安全知識的了解程度,進行了隨機抽樣調查,并繪制成如圖所示的兩幅統計圖,請根據統計圖中的信息,解答下列問題:
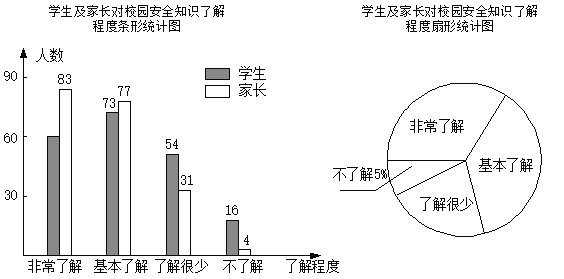
(1)參與調查的學生及家長共有 人;
(2)在扇形統計圖中,“基本了解”所對應的圓心角的度數是 ;
(3)在條形統計圖中,“非常了解”所對應的學生人數是 ;
(4)若全校有1200名學生,請你估計對“校園安全”知識達到“非常了解”和“基本了解”的學生共有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖, AB∥CD,∠1=∠2,那么∠E和∠F相等嗎? 為什么?
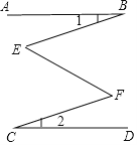
【答案】相等,理由見解析.
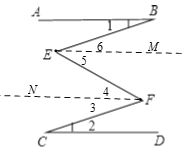
【解析】試題分析:分別過E、F 點作CD的平行線EM、FN,根據平行線的性質得CD∥FN∥EM∥AB,則∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
試題解析:分別過E、F 點作CD的平行線EM、FN,如圖
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.
【題型】解答題
【結束】
26
【題目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)請用字母表示第n個等式,并驗證你的發現.
(3)利用(2)中你的發現,求20+21+22+23+…+22016+22017的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
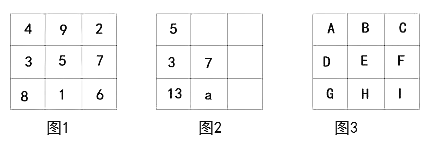
【題目】將9個數填入幻方的九個格中,使處于同一橫行、同一豎列、同一斜對角線上的三個數的和相等,如圖1所示。
(1)如圖2所示,求![]() 的值;
的值;
(2)如圖3所示:
①若![]() 求整式D;
求整式D;
②若![]() 求這九個整式的和是多少。
求這九個整式的和是多少。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD內接于⊙O,點E是 ![]() 上一點(不與A、B重合),點F是
上一點(不與A、B重合),點F是 ![]() 上一點,連接OE,OF,分別與AB,BC交于點G,H,有下列結論:
上一點,連接OE,OF,分別與AB,BC交于點G,H,有下列結論:
① ![]() =
= ![]() ;
;
②△OGH是等腰三角形;
③四邊形OGBH的面積隨著點E位置的變化而變化;
④若BG=1﹣ ![]() ,則BG,GE,
,則BG,GE, ![]() 圍成的面積是
圍成的面積是 ![]() +
+ ![]() .
.
其中正確的是(把所有正確結論的序號都填上)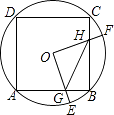
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com