
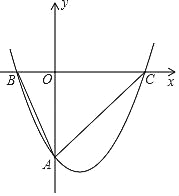
【題目】如圖,經過點A(0,﹣4)的拋物線y=![]() x2+bx+c與x軸相交于點B(﹣2,0)和C,O為坐標原點.
x2+bx+c與x軸相交于點B(﹣2,0)和C,O為坐標原點.
(1)求拋物線解析式;
(2)將拋物線y=![]() x2+bx+c向上平移
x2+bx+c向上平移![]() 個單位長度,再向左平移m(m>0)個單位長度,得到新拋物線,若新拋物線的頂點P在△ABC內,求m的取值范圍.
個單位長度,再向左平移m(m>0)個單位長度,得到新拋物線,若新拋物線的頂點P在△ABC內,求m的取值范圍.
【答案】(1)y=![]() x2﹣x﹣4;(2)0<m<
x2﹣x﹣4;(2)0<m<![]() .
.
【解析】
(1)該拋物線的解析式中只有兩個待定系數,只需將A、B兩點坐標代入即可得解;
(2)首先根據平移條件表示出移動后的函數解析式,從而用m表示出該函數的頂點坐標,將其代入直線AB、AC的解析式中,即可確定P在△ABC內時m的取值范圍.
(1)將A(0,﹣4)、B(﹣2,0)代入拋物線y=![]() x2+bx+c中,得:
x2+bx+c中,得:
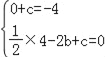 ,
,
解得:![]() ,
,
故拋物線的解析式:y=![]() x2﹣x﹣4.
x2﹣x﹣4.
(2)由題意,新拋物線的解析式可表示為:y=![]() (x+m)2﹣(x+m)﹣4+
(x+m)2﹣(x+m)﹣4+![]() ,即:y=
,即:y=![]() x2+(m﹣1)x+
x2+(m﹣1)x+![]() m2﹣m﹣
m2﹣m﹣![]() ;
;
它的頂點坐標P:(1﹣m,﹣1);
由(1)的拋物線解析式可得:C(4,0);
設直線AC的解析式為y=kx+b(k≠0),把x=4,y=0代入,
∴4k+b=0,b=﹣4,
∴y=x﹣4.
同理直線AB:y=﹣2x﹣4;
當點P在直線AB上時,﹣2(1﹣m)﹣4=﹣1,解得:m=![]() ;
;
當點P在直線AC上時,(1﹣m)﹣4=﹣1,解得:m=﹣2;
∴當點P在△ABC內時,﹣2<m<![]() ;
;
又∵m>0,
∴符合條件的m的取值范圍:0<m<![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:初中數學 來源: 題型:
【題目】一輛貨車早晨7∶00出發,從甲地駛往乙地送貨.如圖是貨車行駛路程y(km)與行駛時間x(h)的完整的函數圖像(其中點B、C、D在同一條直線上),小明研究圖像得到了以下結論:
①甲乙兩地之間的路程是100 km;
②前半個小時,貨車的平均速度是40 km/h;
③8∶00時,貨車已行駛的路程是60 km;
④最后40 km貨車行駛的平均速度是100 km/h;
⑤貨車到達乙地的時間是8∶24,
其中,正確的結論是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B兩種機器人都被用來搬運化工原料,A型機器人比B型機器人每小時多搬運30kg,A型機器人搬運900kg與B型機器人搬運600kg所用時間相等,兩種機器人每小時分別搬運多少化工原料?
查看答案和解析>>
科目:初中數學 來源: 題型:
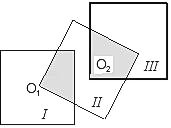
【題目】如圖,有若干個邊長為2的正方形,若正方形的一個頂點是正方形Ⅰ的中心O1,如圖所示,類似的正方形Ⅲ的一個頂點是正方形Ⅱ的中心O2,并且正方形Ⅰ與正方形Ⅲ不重疊,如果若干個正方形都按這種方法拼接,需要m個正方形能使拼接處的圖形的陰影部分的面積等于一個正方形的面積.現有一拋物線y=mx2+nx+3,其頂點在x軸上,則該拋物線的對稱軸為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
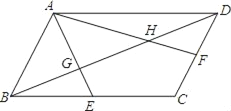
【題目】如圖,在平行四邊形ABCD中,E、F分別是BC邊,CD邊的中點,AE、AF分別交BD于點G,H,設△AGH的面積為S1,平行四邊形ABCD的面積為S2,則S1:S2的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是∠AOB內任意一點,且∠AOB=40°,點M和點N分別是射線OA和射線OB上的動點,當△PMN周長取最小值時,則∠MPN的度數為( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是等邊三角形,以BC為直徑的半圓O與邊AB相交于點D,DE⊥AC,垂足為點E.
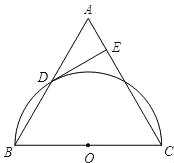
(1)判斷DE與⊙O的位置關系,并證明你的結論;
(2)若AE=1,求⊙O的直徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com