
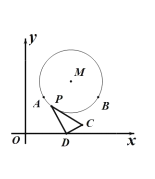
【題目】如圖,在平面直角坐標系中,點![]() 、點
、點![]() 在半徑為
在半徑為![]() 的
的![]() 上,
上,![]() 為
為![]() 上一動點,
上一動點,![]() 為
為![]() 軸上一定點,
軸上一定點,![]() 且
且![]() 當點
當點![]() 從
從![]() 點逆時針運動到
點逆時針運動到![]() 點時,
點時,![]() 點的運動路徑長是( )
點的運動路徑長是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
結合圖形及tan∠DPC=tan30°=![]() ,且D為定點,分析動點P與動點C運動具有相關性,其運動的路徑均為圓弧,長度比為對應線段的比,求出點P的運動弧長即可求解.
,且D為定點,分析動點P與動點C運動具有相關性,其運動的路徑均為圓弧,長度比為對應線段的比,求出點P的運動弧長即可求解.
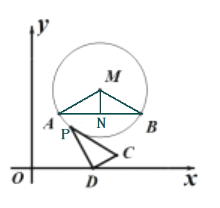
解:連接MA,MB,AB,過點M作AB的垂線交AB于N,則AN=BN=![]() AB=
AB=![]() ,而MA=MB=
,而MA=MB=![]() ,
,
在直角三角形AMN中,∵sin∠AMN=![]() ,
,
∴∠AMN=60°,故∠AMB=120°,
點P在圓上從![]() 點逆時針運動到
點逆時針運動到![]() 點時,其所走的弧長為
點時,其所走的弧長為![]() ,
,
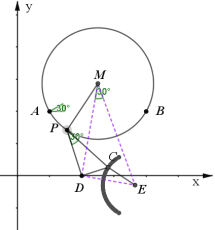
在![]() PDC中,
PDC中,![]() ,故tan
,故tan![]() =
=![]() ,且結合圖形及P、C兩點的相關性,知P、C的運動路徑均為圓弧,且路徑長度比為其對應得線段的比,即為
,且結合圖形及P、C兩點的相關性,知P、C的運動路徑均為圓弧,且路徑長度比為其對應得線段的比,即為![]() ,故點C的運動路徑長為:
,故點C的運動路徑長為:![]() .
.
關于點C的路徑簡證:如圖連接DM,以DM為直角邊,構造一個直角三角形DME,使∠DME=30°,∠MDE=90°,連接CE,則![]() ,而易知∠PDM=∠CDE,所以
,而易知∠PDM=∠CDE,所以![]() PDM∽
PDM∽![]() CDE,故有
CDE,故有![]() ,因此得到CE=
,因此得到CE=![]() PM=1,而通過構造知點E為定點,故點C的路徑為以點E為圓心,1為半徑的圓弧.
PM=1,而通過構造知點E為定點,故點C的路徑為以點E為圓心,1為半徑的圓弧.
故選:A.


科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠B=90°,AB=BC=12cm,點D從點A出發沿邊AB以2cm/s的速度向點B移動,移動過程中始終保持DE∥BC,DF∥AC(點E、F分別在AC、BC上).設點D移動的時間為t秒.
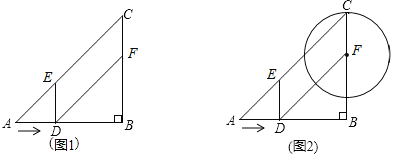
(1)試判斷四邊形DFCE的形狀,并說明理由;
(2)當t為何值時,四邊形DFCE的面積等于20cm2?
(3)如圖2,以點F為圓心,FC的長為半徑作⊙F,在運動過程中,當⊙F與四邊形DFCE只有1個公共點時,請直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業接到一批防護服生產任務,按要求15天完成,已知這批防護服的出廠價為每件80元,為按時完成任務,該企業動員放假回家的工人及時返回加班趕制.該企業第![]() 天生產的防護服數量為
天生產的防護服數量為![]() 件,
件,![]() 與
與![]() 之間的關系可以用圖中的函數圖象來刻畫.
之間的關系可以用圖中的函數圖象來刻畫.

(1)直接寫出![]() 與
與![]() 的函數關系式________;
的函數關系式________;
(2)由于疫情加重,原材料緊缺,防護服的成本前5天為每件50元,從第6天起每件防護服的成本比前一天增加2元,設第![]() 天創造的利潤為
天創造的利潤為![]() 元,直接利用(1)的結論,求
元,直接利用(1)的結論,求![]() 與
與![]() 之間的函數表達式,并求出第幾天的利潤最大,最大利潤是多少元?(利潤=出廠價-成本)
之間的函數表達式,并求出第幾天的利潤最大,最大利潤是多少元?(利潤=出廠價-成本)
查看答案和解析>>
科目:初中數學 來源: 題型:
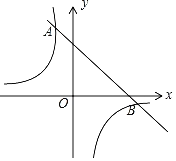
【題目】如圖,一次函數y=k1x+b的圖象與反比例函數y=![]() 的圖象相交于A、B兩點,其中點A的坐標為(﹣1,4),點B的坐標為(4,n).
的圖象相交于A、B兩點,其中點A的坐標為(﹣1,4),點B的坐標為(4,n).
(1)求這兩個函數的表達式;
(2)根據圖象,直接寫出滿足k1x+b>![]() 的x的取值范圍.
的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 的直徑
的直徑![]() ,
,![]() 、
、![]() 為圓周上兩點,且
為圓周上兩點,且![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() .
.
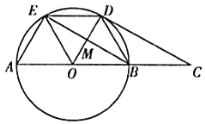
(1)求證:![]() 為
為![]() 切線;
切線;
(2)填空:①當四邊形![]() 為菱形,則
為菱形,則![]() 的度數為________;
的度數為________;
②當![]() 時,四邊形
時,四邊形![]() 的面積為________.
的面積為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是由邊長為![]() 的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形
的小正方形構成的網格,每個小正方形的頂點叫做格點.四邊形![]() 的頂點在格點上,點
的頂點在格點上,點![]() 是邊
是邊![]() 邊上的一點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
邊上的一點.請選擇適當的格點,用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
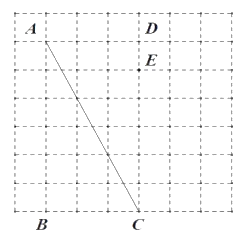
(1)①過![]() 作
作![]() 交
交![]() 邊于
邊于![]() ;
;
②過![]() 作
作![]() 于
于![]() 點;
點;
③在![]() 上作線段
上作線段![]()
(2)在(1)的條件下,連![]() ,若
,若![]() 為
為![]() 邊上的動點,在網格中求作一條線段
邊上的動點,在網格中求作一條線段![]() 等于
等于![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某社區購買甲、乙兩種樹苗進行綠化,購買一棵甲種樹苗的價錢比購買一棵乙種樹苗的價錢多 10 元錢,已知購買 20 棵甲種樹苗、30 棵乙種樹苗共需 1 200 元錢.
(1)求購買一棵甲種、一棵乙種樹苗各多少元?
(2)社區決定購買甲、乙兩種樹苗共 400 棵,總費用不超過 10 600 元,那么該社區最多可以購買多少棵甲種樹苗?
查看答案和解析>>
科目:初中數學 來源: 題型:
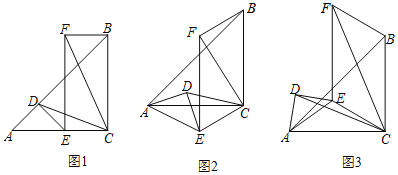
【題目】已知△ACB和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,以CE、BC為邊作平行四邊形CEFB,連CD、CF.
(1)如圖1,當E、D分別在AC和AB上時,求證:CD=![]() CF;
CF;
(2)如圖2,△ADE繞點A旋轉一定角度,判斷(1)中CD與CF的數量關系是否依然成立,并加以證明;
(3)如圖3,AE=![]() ,AB=
,AB=![]() ,將△ADE繞A點旋轉一周,當四邊形CEFB為菱形時,直接寫出CF的長.
,將△ADE繞A點旋轉一周,當四邊形CEFB為菱形時,直接寫出CF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某中學學生課余生活情況,對喜愛看課外書、體育活動、看電視、社會實踐四個方面的人數進行調查統計,現從該校隨機抽取n名學生作為樣本,采用問卷調查的方式收集數據![]() 參與問卷調查的每名學生只能選擇其中一項
參與問卷調查的每名學生只能選擇其中一項![]() ,并根據調查得到的數據繪制成了如圖所示的兩幅不完整的統計圖,由圖中提供的信息,解答下列問題:
,并根據調查得到的數據繪制成了如圖所示的兩幅不完整的統計圖,由圖中提供的信息,解答下列問題:

![]() 補全條形統計圖;
補全條形統計圖;
![]() 若該校共有學生2400名,試估計該校喜愛看電視的學生人數.
若該校共有學生2400名,試估計該校喜愛看電視的學生人數.
![]() 若調查到喜愛體育活動的4名學生中有3名男生和1名女生,現從這4名學生中任意抽取2名,求恰好抽到2名男生的概率.
若調查到喜愛體育活動的4名學生中有3名男生和1名女生,現從這4名學生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com