
【題目】中國古代有二十四節氣歌,“春雨驚春清谷天,夏滿芒夏暑相連.秋處露秋寒霜降,冬雪雪冬小大寒.”它是為便于記憶我國古時歷法中二十四節氣而編成的小詩歌,流傳至今.節氣指二十四時節和氣候,是中國古代訂立的一種用來指導農事的補充歷法,是中國古代勞動人民長期經驗的積累和智慧的結晶.其中第一個字“春”是指立春,為春季的開始,但在氣象學上的入春日是有嚴格定義的,即連續5天的日平均氣溫穩定超過10℃又低于22℃,才算是進入春天,其中,5天中的第一天即為入春日.例如:2014年3月13日至18日,北京的日平均氣溫分別為9.3℃,11.7℃,12.7℃,11.7℃,12.7℃和12.3℃,即從3月14日開始,北京日平均氣溫已連續5天穩定超過10℃,達到了氣象學意義上的入春標準.因此可以說2014年3月14日為北京的入春日. 日平均溫度是指一天24小時的平均溫度.氣象學上通常用一天中的2時、8時、14時、20時4個時刻的氣溫的平均值作為這一天的日平均氣溫(即4個氣溫相加除以4),結果保留一位小數.
如表是北京順義2017年3月28日至4月3日的氣溫記錄及日平均氣溫(單位:℃)
時間 | 2時 | 8時 | 14時 | 20時 | 平均氣溫 |
3月28日 | 6 | 8 | 13 | 11 | 9.5 |
3月29日 | 7 | 6 | 17 | 14 | a |
3月30日 | 7 | 9 | 15 | 12 | 10.8 |
3月31日 | 8 | 10 | 19 | 13 | 12.5 |
4月1日 | 8 | 7 | 18 | 15 | 12 |
4月2日 | 11 | 7 | 22 | 16 | 14 |
4月3日 | 13 | 11 | 21 | 17 | 15.5 |
根據以上材料解答下列問題:
(1)求出3月29日的日平均氣溫a;
(2)采用適當的統計圖將這7天的日平均氣溫的變化情況表示出來;
(3)請指出2017年的哪一天是北京順義在氣象學意義上的入春日.
【答案】
(1)解:a= ![]() =11(℃)
=11(℃)
(2)解:如圖所示,
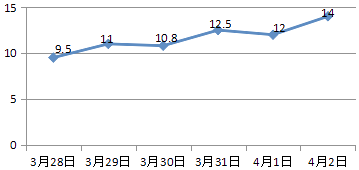
(3)解:2017年的3月29日是北京順義在氣象學意義上的入春日
【解析】(1)根據算術平均數的求法即可得到結論;(2)根據題意繪制統計圖;(3)根據題意即可得到結論.
【考點精析】本題主要考查了統計圖的選擇和算術平均數的相關知識點,需要掌握條形統計圖便于直觀了解數據的大小及不同數據的差異;折線統計圖便于直觀了解數據的變化趨勢,同時也便于了解數據的多少;扇形統計圖便于直觀了解各部分數量與總數的百分比,以及部分與部分之間的大小關系;總數量÷總份數=平均數.解題關鍵是根據已知條件確定總數量以及與它相對應的總份數才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,已知點E、F在直線AB上,點G在線段CD上,ED與FG交于點H,∠C=∠EFG,∠CED=∠GHD.
(1)求證:CE∥GF;
(2)試判斷∠AED與∠D之間的數量關系,并說明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正五邊形廣場 ![]() 的邊長為
的邊長為 ![]() 米,甲、乙兩個同學做游戲,分別從
米,甲、乙兩個同學做游戲,分別從 ![]() 、
、 ![]() 兩點處同時出發,沿
兩點處同時出發,沿 ![]() 的方向繞廣場行走,甲的速度為
的方向繞廣場行走,甲的速度為 ![]() ,乙的速度為
,乙的速度為 ![]() ,則兩人第一次剛走到同一條邊上時( )
,則兩人第一次剛走到同一條邊上時( )
A. 甲在頂點 ![]() 處 B. 甲在頂點
處 B. 甲在頂點 ![]() 處 C. 甲在頂點
處 C. 甲在頂點![]() 處 D. 甲在頂點
處 D. 甲在頂點![]() 處
處
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究)如圖①,∠AFH和∠CHF的平分線交于點O,EG經過點O且平行于FH,分別與AB、CD交于點E、G.
(1)若∠AFH=60°,∠CHF=50°,則∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度數.
(拓展)如圖②,∠AFH和∠CHI的平分線交于點O,EG經過點O且平行于FH,分別與AB、CD交于點E、G.若∠AFH+∠CHF=α,直接寫出∠FOH的度數.(用含a的代數式表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】Rt△ABC中,∠C=90°,點D、E分別是△ABC邊AC、BC上的點,點P是一動點.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若點P在線段AB上,如圖(1)所示,且∠α=50°,則∠1+∠2= °;
(2)若點P在邊AB上運動,如圖(2)所示,則∠α、∠1、∠2之間的關系為: ;
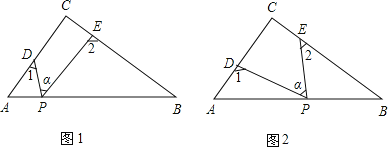
(3)若點P運動到邊AB的延長線上,如圖(3)所示,則∠α、∠1、∠2之間有何關系?猜想并說明理由.
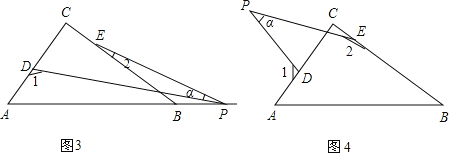
(4)若點P運動到△ABC形外,如圖(4)所示,則∠α、∠1、∠2之間的關系為: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD中,對角線AC,BD相交于點O,AB=AC=AD,∠DAC=∠ABC. 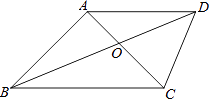
(1)求證:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中:A(1,1),B(-1,1),C(-1,-2),D(1,-2),現把一條長為2 018個單位長度且沒有彈性的細線(線的粗細忽略不計)的一端固定在點A處,并按A→B→C→D→A→…的規律緊繞在四邊形ABCD的邊上,則細線另一端所在位置的點的坐標是________.
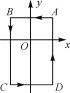
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點E為矩形ABCD外一點,連接AE,DE,且AE=DE,連接EB,EC分別與AD相交于點F,G.
(1)如圖1,求證:∠ABE=∠DCE;
(2)如圖2,若△BCE是等邊三角形,且AE=AB,在不添加任何輔助線的情況下,請直接寫出圖2中四對全等的鈍角三角形.
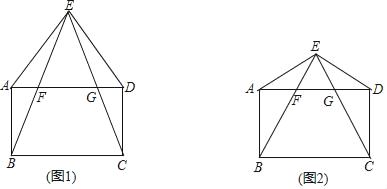
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com