
【題目】對于平面直角坐標系中的任意一點P(a,b),我們定義:當k為常數,且k≠0時,點P′(a+![]() ,ka+b)為點P的“k對應點”.
,ka+b)為點P的“k對應點”.
(1)點P(﹣2,1)的“3對應點”P′的坐標為 ;若點P的“﹣2對應點”P′的坐標為(﹣3,6),且點P的縱坐標為4,則點P的橫坐標a= ;
(2)若點P的“k對應點”P′在第一、三象限的角平分線(原點除外)上,求k值;
(3)若點P在x軸的負半軸上,點P的“k對應點”為P′點,且∠OP'P=30°,求k值.
【答案】(1)(﹣![]() ,﹣5),﹣1;(2)k=1;(3)k=
,﹣5),﹣1;(2)k=1;(3)k=![]() 或﹣
或﹣![]() .
.
【解析】
(1)根據點P的“k對應點”的定義列式計算,得到答案;
(2)根據第一、三象限的角平分線上的點的橫縱坐標相等計算;
(3)根據點P的“k對應點”的定義表示出P′點的坐標,根據直角三角形的性質、正切的定義計算即可.
解:(1)﹣2+![]() =﹣
=﹣![]() ,﹣2×3+1=﹣5,
,﹣2×3+1=﹣5,
則點P(﹣2,1)的“3對應點”P′的坐標為(﹣![]() ,﹣5),
,﹣5),
∵點P的“﹣2對應點”P′的坐標為(﹣3,6),點P的縱坐標為4,
∴﹣2a+4=6,
解得,a=﹣1,即點P的橫坐標a=﹣1,
故答案為:(﹣![]() ,﹣5);﹣1;
,﹣5);﹣1;
(2)∵點P′在第一、三象限的角平分線(原點除外)上,
∴a+![]() =ka+b,
=ka+b,
整理得,(ka+b)(1﹣k)=0,
由題意得,ka+b≠0,
∴1﹣k=0,
解得,k=1;
(3)如圖
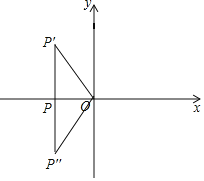
∵點P在x軸的負半軸上,
∴設點P的坐標為(a,0),
則點P的“k對應點”為P′點的坐標為(a,ka),
∴PP′⊥x軸,
∵∠OP'P=30°,
∴![]() =tan30°,
=tan30°,
∴![]() =
=![]() ,
,
解得,k=±![]() ,
,
則點P在x軸的負半軸上,點P的“k對應點”為P′點,∠OP'P=30°時,k=![]() 或﹣
或﹣![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10,BC=![]() ,D為邊AC上一動點(C點除外),把線段BD繞著點D沿著順時針的方向旋轉90°至DE,連接CE,則△CDE面積的最大值為______.
,D為邊AC上一動點(C點除外),把線段BD繞著點D沿著順時針的方向旋轉90°至DE,連接CE,則△CDE面積的最大值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】市實驗中學計劃在暑假第二周的星期一至星期五開展暑假社會實踐活動,要求每位學生選擇兩天參加活動.
(1)甲同學隨機選擇連續的兩天,其中有一天是星期三的概率是 ;
(2)乙同學隨機選擇兩天,其中有一天是星期三的概率是多少?(列表或畫樹形圖或列舉)
查看答案和解析>>
科目:初中數學 來源: 題型:
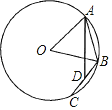
【題目】如圖,已知⊙O的半徑為6,點A、B在⊙O上,∠AOB=60°,動點C在⊙O上(與A、B兩點不重合),連接BC,點D是BC中點,連接AD,則線段AD的最大值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
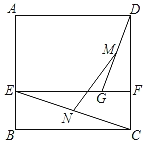
【題目】如圖,已知正方形ABCD的邊長為4,E,F分別為AB,CD邊上的點,且EF∥BC,G為EF上一點,且GF=1,M,N分別為GD,EC的中點,則MN=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個四邊形的對角線把四邊形分成兩個三角形,一個是等邊三角形,另一個是該對角線所對的角為60°的三角形,我們把這條對角線叫做這個四邊形的理想對角線,這個四邊形稱為理想四邊形.
(1)如圖①,在Rt△ABC中∠C=90°,∠B=30°,AC=4,D為AB上一點,AD=2,E為BC中點,連接DE.求證:四邊形ADEC為理想四邊形;
(2)如圖②,△ABC是等邊三角形,若BD為理想對角線,四邊形ABCD為理想四邊形.請畫圖找出符合條件的C點落在怎樣的圖形上;
(3)在(2)的條件下,
①若△BCD為直角三角形,BC=3,求AC的長度;
②如圖③,若CD=x,BC=y,AC=z,請直接寫出x,y,z之間的數量關系.
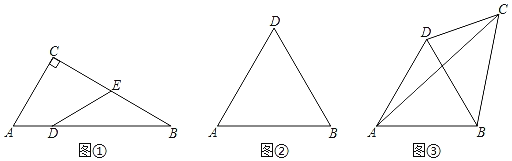
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在四邊形ABCD中,AB∥CD,對角線AC與BD相交于點O,那么下列條件中能判定這個四邊形是矩形的是( )
A.AD=BC,AC=BDB.AC=BD,∠BAD=∠BCD
C.AO=CO,AB=BCD.AO=OB,AC=BD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 與反比例函數
與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() 與點
與點![]() .
.
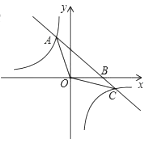
(1)求反比例函數的表達式及![]() 點坐標.
點坐標.
(2)根據圖象回答,在什么范圍時,一次函數的值大于反比例函數的值.
(3)求三角形![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com