【題目】計算下列各題
某廣告公司設計一幅周長為16米的矩形廣告牌，廣告設計費為每平方米2000元，設矩形一邊長為
，面積為
平方米.
（1）求與之間的函數(shù)關系式，并寫出自變量的取值范圍；
（2）設計費能可以達到30000元嗎？為什么？
（3）當是多少米時，設計費最多？最多是多少元？
【答案】（1）
， 
；（2）設計費能達到30000元；（3）當
是4米時，矩形的最大面積為16平方米，設計費最多，最多是32000元.
【解析】
（1）用8-x表示另一邊，即可列式求
與之間的函數(shù)關系式；
（2）能，由2000S=30000，求出x即方程有解且符合題意；
（3）配方為頂點式解析式，即可確定答案.
解：（1）矩形的一邊長為米，周長為16米.另一邊長為
米，
∴
，其中；
（2）能.
理由是：∵設計費為每平方米2000元，∴2000S=30000
∴面積為：
（平方米）
即
，解得
，
；
∴設計費能達到30000元；
（3）∵
，
∴當
時，
，∴
.
∴當是4米時，矩形的最大面積為16平方米，設計費最多，最多是32000元.
科目：初中數(shù)學 來源： 題型：
【題目】已知二次函數(shù)y＝a(x﹣1)2+4的圖象經(jīng)過點(﹣1，0)．
(1)求這個二次函數(shù)的解析式；
(2)判斷這個二次函數(shù)的開口方向，對稱軸和頂點坐標．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
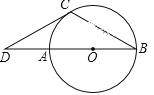
【題目】已知：如圖，AB是⊙O的直徑，BC是弦，∠B=30°，延長BA到D，使∠BDC=30°．
(1)求證：DC是⊙O的切線；
(2)若AB=2，求DC的長．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】某服裝店出售某品牌的棉衣，進價為100元/件，當售價為150元/件時，平均每天可賣30件；為了增加利潤和減少庫存，商店決定降價銷售.經(jīng)調(diào)査，每件每降價1元，則每天可多賣2件.
（1）若每件降價20元，則平均每天可賣______件.
（2）現(xiàn)要想平均每天獲利2000元，且讓顧客得到實惠，求每件棉衣應降價多少元？
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】矩形OABC的邊OA、OC分別在y軸和x軸的正半軸上，且長分別為m、4m，D為AB的中點，拋物線y＝﹣x2+bx+c經(jīng)過點A、點D．
（1）當m＝1時，求拋物線y＝﹣x2+bx+c的函數(shù)關系式；
（2）延長BC至點E，連接OE，若OD平分∠AOE，拋物線與線段CE相交，求拋物線的頂點P到達最高位置時的坐標．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖（1），某數(shù)學活動小組經(jīng)探究發(fā)現(xiàn)：在⊙O中，直徑AB與弦CD相交于點P,此時PA· PB=PC·PD
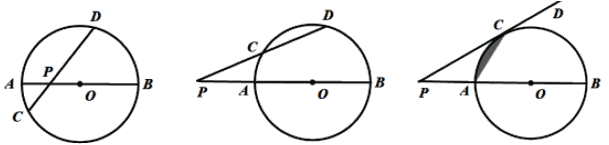
（1）如圖（2），若AB與CD相交于圓外一點P, 上面的結論是否成立？請說明理由．
（2）如圖（3）,將PD繞點P逆時針旋轉(zhuǎn)至與⊙O相切于點C, 直接寫出PA、PB、PC之間的數(shù)量關系．
（3）如圖（3），直接利用（2）的結論，求當 PC= 
,PA=1時,陰影部分的面積．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
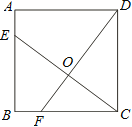
【題目】如圖,已知正方形ABCD的邊長為4，點E、F分別在邊AB、BC上，且AE=BF=1，CE、DF交于點O.下列結論：①∠DOC=90°, ②OC=OE， ③tan∠OCD =
，④
中，正確的有（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
