
右圖是轟炸機群一個飛行隊形,如果最后兩架轟炸機的平面坐標分別是A(-2,1)和B(-2,-3),那么第一架轟炸機C的平面坐標是 。

科目:初中數學 來源: 題型:
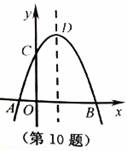
如圖,拋物線y=-x2+2x+m+1交x軸于點A(a,0)和B(B,0),交y軸于點C,
拋物線的頂點為D.下列四個判斷:①當x>0時,y>0;②若a=-1,則b=4;③拋物
線上有兩點P(x1,y1)和Q(x2,y2),若x1<1< x2,且x1+ x2>2,則y1> y2;④點C關于
拋物線對稱軸的對稱點為E,點G,F分別在x軸和y軸上,當m=2時,四邊形EDFG
周長的最小值為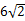 ,其中正確判斷的序號是( )
,其中正確判斷的序號是( )
(A)① (B)②(C)③ (D)④
查看答案和解析>>
科目:初中數學 來源: 題型:
要估計魚塘中的魚數,養魚者首先從魚塘中打撈了50條魚,在每條魚身上做好記號后把這些魚放歸魚塘,再從魚塘中打撈100條,發現只有兩條魚是剛才做了記號的魚,假設在魚塘內魚均勻分布,那么估計這個魚塘的魚數約為( )
A、5000條 B、2500條 C、1750條 D、1250條
查看答案和解析>>
科目:初中數學 來源: 題型:
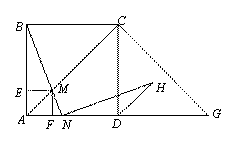
如圖,在邊長為2的正方形ABCD中,G是AD延長線上的一點,且DG=AD,動點M從A出發,以每秒1個單位的速度沿著A→C→G的路線向G點勻速運動(M不與A、G重合),設運動時間為t秒。連接BM并延長交AG于N。
(1)是否存在點M,使△ABM為等腰三角形?若存在,分析點M的位置;若不存在,請說明理由;
(2)當點N在AD邊上時,若BN⊥HN,NH交∠CDG的平分線于H,求證:BN=NH;
(3)過點M分別用AB、AD的垂線,垂足分別為E、F,矩形AEMF與△ACG重疊部分的面積為S,求S的最大值。
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
在平面直角坐標系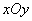 中,
中, 的半徑為r,P是與圓心C不重合的點,點P關于
的半徑為r,P是與圓心C不重合的點,點P關于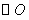 的反稱點的定義如下:若
的反稱點的定義如下:若 在射線CP上存在一點
在射線CP上存在一點 ,滿足
,滿足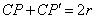 ,則稱
,則稱 為點P關于
為點P關于 的反稱點,下圖為點P及其
的反稱點,下圖為點P及其 關于
關于 的反稱點
的反稱點 的示意圖。
的示意圖。
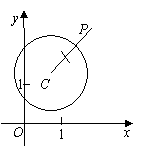 |
(1)當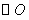 的半徑為1時。
的半徑為1時。
①分別判斷點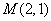 ,
,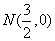 ,
,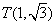 關于
關于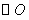 的反稱點是否存在,若存
的反稱點是否存在,若存 在?
在?
求其坐標;
②點P在直線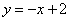 上,若點P關于
上,若點P關于 的反稱點
的反稱點 存在,且點
存在,且點 不在x軸上,求點P的橫坐標的取值范圍;
不在x軸上,求點P的橫坐標的取值范圍;
(2)當 的圓心在x軸上,半徑為1,直線
的圓心在x軸上,半徑為1,直線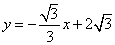 與x軸,y軸分別交于點A,B,若線段AB上存在點P,使得點P關于
與x軸,y軸分別交于點A,B,若線段AB上存在點P,使得點P關于 的反稱點
的反稱點 在
在 的內部,求圓心C的橫坐標的取值范圍。
的內部,求圓心C的橫坐標的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com