
【題目】如圖在平面直角坐標(biāo)系中,一次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖象經(jīng)過
的圖象經(jīng)過![]() ,
,![]() 兩點,且與
兩點,且與![]() 軸的負(fù)半軸交于點
軸的負(fù)半軸交于點![]() ,動點
,動點![]() 在直線
在直線![]() 下方的二次函數(shù)圖象上.
下方的二次函數(shù)圖象上.
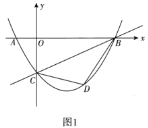
(1)求二次函數(shù)的表達(dá)式;
(2)如圖1,連接![]() ,
,![]() ,設(shè)
,設(shè)![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值;
的最大值;
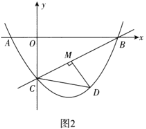
(3)如圖2,過點![]() 作
作![]() 于點
于點![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 中的某個角恰好等于
中的某個角恰好等于![]() 的2倍?若存在,直接寫出點
的2倍?若存在,直接寫出點![]() 的橫坐標(biāo);若不存在,請說明理由.
的橫坐標(biāo);若不存在,請說明理由.
【答案】1)![]() ;(2)S最大值為4;(3)存在,點D的橫坐標(biāo)為2或
;(2)S最大值為4;(3)存在,點D的橫坐標(biāo)為2或![]()
【解析】
(1)根據(jù)題意得到B、C兩點的坐標(biāo),設(shè)拋物線的解析式為![]() ,將點C的坐標(biāo)代入求得m的值即可;
,將點C的坐標(biāo)代入求得m的值即可;
(2)過點D作DF⊥x軸,交BC與點F,設(shè)![]() ,則
,則![]() ,然后列出S與x的關(guān)系式,最后利用配方法求得其最大值即可;
,然后列出S與x的關(guān)系式,最后利用配方法求得其最大值即可;
(3)根據(jù)勾股定理的逆定理得到△ABC是以∠ACB為直角的直角三角形,取AB的中點E,EA=EC=EB=![]() ,過D作Y軸的垂線,垂足為R,交AC的延線于G,設(shè)
,過D作Y軸的垂線,垂足為R,交AC的延線于G,設(shè)![]() ,則DR=x,
,則DR=x,![]() ,最后,分為∠DCM=2∠BAC和∠MDC=2∠BAC兩種情況列方程求解即可.
,最后,分為∠DCM=2∠BAC和∠MDC=2∠BAC兩種情況列方程求解即可.
:(1)把x=0代入![]() 得y=-2,
得y=-2,
∴C(0,-2).
把y=0代![]() 得x=4,
得x=4,
∴B(4,0),
設(shè)拋物線的解析式為![]() ,將C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
,將C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
∴拋物線的解析式![]() ,即
,即![]() ;
;
(2)如圖所示:過點D作DF⊥x軸,交BC與點F.
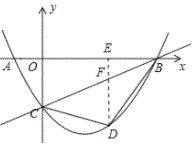
設(shè)![]() ,則
,則![]() ,
,![]() ,
,
∴![]() ,
,
∴當(dāng)x=2時,S有最大值,最大值為4.
(3)如圖所示:過點D作DR⊥y垂足為R,DR交BC與點G.
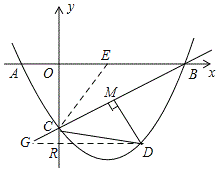
∵A(-1,0),B(4,0),C(0,-2),
∴![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC為直角三角形.
取AB的中點E,連接CE,則CE=BE,
∴∠OEC=2∠ABC.
∴![]() ,
,
當(dāng)∠MCD=2∠ABC時,則tan∠CDR=tan∠ABC= ![]() ,
,
設(shè)![]() ,則DR=x,
,則DR=x,![]() ,
,
∴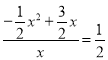 ,解得:x=0(舍去)或x=2.
,解得:x=0(舍去)或x=2.
∴點D的橫坐標(biāo)為2.
當(dāng)∠CDM=2∠ABC時,設(shè)MD=3k,CM=4k,CD=5k.
∵tan∠MGD= ![]() ,
,
∴GM=6k,![]() ,
,
∴GC=MG-CM=2k,
∴![]() ,
,
∴![]() ,
,
∴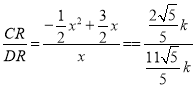 ,整理得:
,整理得:![]() ,
,
解得:x=0(舍去)或x=![]() .
.
∴點D的橫坐標(biāo)為![]() ,
,
綜上所述,當(dāng)點D的橫坐標(biāo)為2或![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某次數(shù)學(xué)競賽中有5道選擇題,每題1分,每道題在![]() 、
、![]() 、
、![]() 三個選項中,只有一個是正確的.下表是甲、乙、丙、丁四位同學(xué)每道題填涂的答案和這5道題的得分:
三個選項中,只有一個是正確的.下表是甲、乙、丙、丁四位同學(xué)每道題填涂的答案和這5道題的得分:
第一題 | 第二題 | 第三題 | 第四題 | 第五題 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)則甲同學(xué)錯的是第 題;
(2)丁同學(xué)的得分是 ;
(3)如果有一個同學(xué)得了1分,他的答案可能是 (寫出一種即可).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
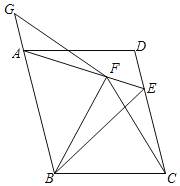
【題目】在平行四邊形ABCD中,以AB為邊作等邊△ABE,點E在CD上,以BC為邊作等邊△BCF,點F在AE上,點G在BA延長線上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面積;
(2)求證:BE=AG+CE.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網(wǎng)格中,已知格點四邊形ABCD(頂點是網(wǎng)格線的交點)和格點O.

(1)將四邊形ABCD先向左平移4個單位長度,再向下平移6個單位長度,得到四邊形A1B1C1D1,畫出平移后的四邊形A1B1C1D1,(點A,B,C,D的對應(yīng)點分別為點A1,B1,C1,D1);
(2)將四邊形ABCD繞點O逆時針旋轉(zhuǎn)90°,得到四邊形A2B2C2D2,畫出旋轉(zhuǎn)后的四邊形A2B2C2D2(點A、B,C,D的對應(yīng)點分別為點A2,B2,C2,D2);
(3)填空:點C2到A1D1的距離為_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線y=ax2+bx+c交x軸于A(﹣1,0),B(3,0),交y軸的負(fù)半軸于C,頂點為D.下列結(jié)論:①2a+b=0;②2c<3b;③當(dāng)m≠1時,a+b<am2+bm;④當(dāng)△ABD是等腰直角三角形時,則a=![]() ;⑤當(dāng)△ABC是等腰三角形時,a的值有3個.其中正確的有( )個.
;⑤當(dāng)△ABC是等腰三角形時,a的值有3個.其中正確的有( )個.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】點![]() ,
,![]() 分別是
分別是![]() 的邊
的邊![]() 、
、![]() 延長線上的點,
延長線上的點,![]() 的延長線交
的延長線交![]() 于
于![]() .
.
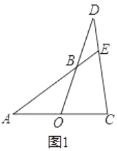
(1)如圖1,![]() ,
,![]() ,求證:
,求證:![]() ;
;
(2)如圖2,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
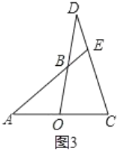
(3)如圖3,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“食品安全”受到全社會的廣泛關(guān)注,育才中學(xué)對部分學(xué)生就食品安全知識的了解程度,采用隨機(jī)抽樣調(diào)查的方式,并根據(jù)收集到的信息進(jìn)行統(tǒng)計,繪制了下面的兩幅尚不完整的統(tǒng)計圖,請你根據(jù)統(tǒng)計圖中所提供的信息解答下列問題:
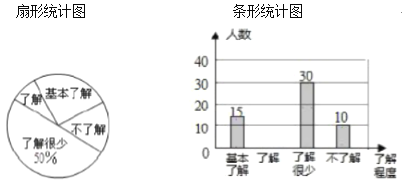
(1)接受問卷調(diào)查的學(xué)生共有________人,扇形統(tǒng)計圖中“基本了解”部分所對應(yīng)扇形的圓心角為_________![]() ;
;
(2)請補(bǔ)全條形統(tǒng)計圖;
(3)若對食品安全知識達(dá)到“了解”程度的學(xué)生中,男、女生的比例恰為![]() ,現(xiàn)從中隨機(jī)抽取
,現(xiàn)從中隨機(jī)抽取![]() 人參加食品安全知識競賽,則恰好抽到
人參加食品安全知識競賽,則恰好抽到![]() 個男生和
個男生和![]() 個女生的概率________.
個女生的概率________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,A點的坐標(biāo)為(﹣1,5),B點的坐標(biāo)為(3,3),C點的坐標(biāo)為(5,3),D點的坐 標(biāo)為(3,﹣1),小明發(fā)現(xiàn):線段AB與線段CD存在一種特殊關(guān)系,即其中一條線段繞著某點旋轉(zhuǎn)一個角度可以得到另一條線段,你認(rèn)為這個旋轉(zhuǎn)中心的坐標(biāo)是_____________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
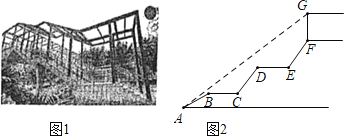
【題目】為了方便學(xué)生在上下學(xué)期間安全過馬路,南岸區(qū)政府決定在南開(融僑)中學(xué)校門口修建人行天橋(如圖1),其平面圖如圖2所示,初三(8)班的學(xué)生小劉想利用所學(xué)知識測量天橋頂棚距地面的高度.天橋入口A點有一臺階AB=2m,其坡角為30°,在AB上方有兩段平層BC=DE=1.5m,且BC,DE與地面平行,BC,DE上方又緊接臺階CD,EF,其長度相等且坡度均為i=4:3,頂棚距天橋距離FG=2m,且小劉從入口A點測得頂棚頂端G的仰角為37°,請根據(jù)以上數(shù)據(jù),幫小劉計算出頂端G點距地面高度為( )m.(結(jié)果保留一位小數(shù),參考數(shù)據(jù):![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com