
【題目】已知兩個單項式﹣2a2bm+1與na2b4的和為0,則m+n的值是 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】觀察下列 ![]() 個命題:其中真命題是( ).
個命題:其中真命題是( ).
⑴三角形的外角和是 ![]() ;⑵三角形的三個內角中至少有兩個銳角;⑶直角三角形兩銳角互余;⑷相等的角是對頂角.
;⑵三角形的三個內角中至少有兩個銳角;⑶直角三角形兩銳角互余;⑷相等的角是對頂角.
A.( ![]() )(
)( ![]() )
)
B.( ![]() )(
)( ![]() )
)
C.( ![]() )(
)( ![]() )
)
D.( ![]() )(
)( ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知坐標平面內的點A(-2,5),若將平面直角坐標系先向右平移3個單位長度,再向上平移4個單位長度,則點A在平移后的坐標系中的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知拋物線y=x2+bx+c與x軸交于A、B兩點(點A在點B左側),與y軸交于點C(0,-3),對稱軸是直線x=1,直線BC與拋物線的對稱軸交于點D.
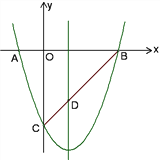
(1)求拋物線的函數表達式;
(2)求直線BC的函數表達式;
(3)點E為y軸上一動點,CE的垂直平分線交CE于點F,交拋物線于P、Q兩點,且點P在第三象限.
①當線段PQ ![]() 時,求tan∠CED的值;
時,求tan∠CED的值;
②當以C、D、E為頂點的三角形是直角三角形時,請直接寫出點P的坐標.
(參考公式:拋物線![]() 的頂點坐標是
的頂點坐標是 )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD為菱形,點P為對角線BD上的一個動點.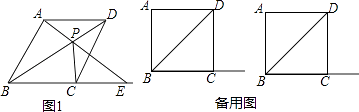
(1)如圖1,連接AP并延長交BC的延長線于點E,連接 PC,求證:∠AEB=∠PCD.
(2)如圖1,當PA=PD且PC⊥BE時,求∠ABC的度數.
(3)連接AP并延長交射線BC于點E,連接 PC,若∠ABC=90°且△PCE是等腰三角形,求∠PEC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b與反比例函數 ![]() 的圖像相交于A(2,3),B(﹣3,n)兩點.
的圖像相交于A(2,3),B(﹣3,n)兩點. 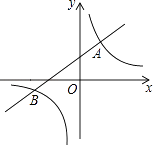
(1)求一次函數與反比例函數的解析式.
(2)根據所給條件,請直接寫出不等式kx+b> ![]() 的解集.
的解集.
(3)連接OA、OB,求S△ABO .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com