
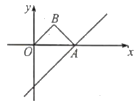
【題目】如圖,直線y=x﹣4與x軸交于點A,以OA為斜邊在x軸上方作等腰Rt△OAB,并將Rt△AOB沿x軸向右平移,當點B落在直線y=x﹣4上時,Rt△OAB掃過的面積是__.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中點![]() 的坐標為(1,0),過點
的坐標為(1,0),過點![]() 作x軸的垂線交直線y=2x于
作x軸的垂線交直線y=2x于![]() ,過點
,過點![]() 作直線y=2x的垂線交x軸于
作直線y=2x的垂線交x軸于![]() ,過點
,過點![]() 作x軸的垂線交直線y=2x于
作x軸的垂線交直線y=2x于![]() …,依此規律,則
…,依此規律,則![]() 的坐標為___________.
的坐標為___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理是人類最偉大的十個科學發現之一,西方國家稱之為畢達哥拉斯定理,但遠在畢達哥拉斯出生之前,這一定理早已被人們所利用,世界上各個文明古國都對勾股定理的發現和研究作出過貢獻(希臘、中國、埃及、巴比倫、印度等),特別是定理的證明,據說有400余種方法.其中在《幾何原本》中有一種證明勾股定理的方法:如圖所示,作CG⊥FH,垂足為G,交AB于點P,延長FA交DE于點S,然后將正方形ACED、正方形BCNM作等面積變形,得S正方形ACED=SACQS,S正方形BCNM=SBCQT,這樣就可以完成勾股定理的證明.對于該證明過程,下列結論錯誤的是( )
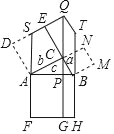
A. △ADS≌△ACB B. SACQS=S矩形APGF
C. SCBTQ=S矩形PBHG D. SE=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
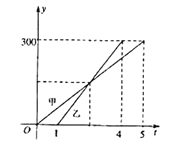
【題目】甲、乙兩車從![]() 城出發勻速行駛至
城出發勻速行駛至![]() 城在個行駛過程中甲乙兩車離開
城在個行駛過程中甲乙兩車離開![]() 城的距離
城的距離![]() (單位:千米)與甲車行駛的時間
(單位:千米)與甲車行駛的時間![]() (單位:小時)之間的函數關系如圖所示.則下列結論: ①
(單位:小時)之間的函數關系如圖所示.則下列結論: ①![]() 兩城相距
兩城相距![]() 千米;②乙車比甲車晚出發
千米;②乙車比甲車晚出發![]() 小時,卻早到
小時,卻早到![]() 小時;③乙車出發后
小時;③乙車出發后![]() 小時追上甲車;④在乙車行駛過程中.當甲、乙兩車相距
小時追上甲車;④在乙車行駛過程中.當甲、乙兩車相距![]() 千米時,
千米時,![]() 或
或![]() ,其中正確的結論是_________.
,其中正確的結論是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A、B、C是直線l上的三個點,線段AB=8厘米.
(1)若AB=2BC,求線段AC的長度;
(2)若點C是線段AB的中點,點P、Q是直線l上的兩個動點,點P的速度為1厘米/秒,點Q的速度為2厘米/秒.點P、Q分別從點C、B同時出發在直線上運動,則經過多少秒時線段PQ的長為5厘來?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下是八(1)班學生身高的統計表和扇形統計圖,請回答以下問題:
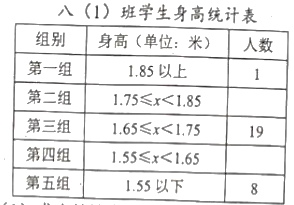
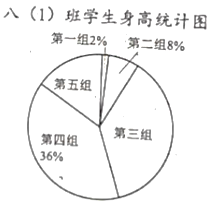
(1)求出統計表和統計圖缺的數據.
(2)八(1)班學生身高這組數據的中位數落在第幾組?
(3)如果現在八(1)班學生的平均身高是1.63m,已確定新學期班級轉來兩名新同學,新同學的身高分別是1.54m和1.77m,那么這組新數據的中位數落在第幾組?
查看答案和解析>>
科目:初中數學 來源: 題型:
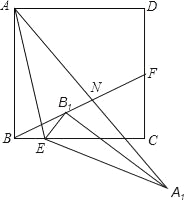
【題目】如圖,正方形ABCD中,AB=4,點E是BC上一點,且tan∠BAE=![]() ,點F是CD的中點,連接AE、BF將△ABE著點E按順時針方向旋轉,使點B落在BF上的B1處位置處,點A經過旋轉落在A1點位置處,連接AA1交BF于點N.
,點F是CD的中點,連接AE、BF將△ABE著點E按順時針方向旋轉,使點B落在BF上的B1處位置處,點A經過旋轉落在A1點位置處,連接AA1交BF于點N.
(1)求證:∠BFC=∠A1 B1F;
(2)說明點N是AA1的中點;
(3)求AN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從邊長為a的正方形中剪掉一個邊長為b的正方形(如圖1),然后將剩余部分拼成一個長方形(如圖2).
(1)探究:上述操作能驗證的等式是 ;(請選擇正確的一個)

A.a2-2ab+b2=(a-b)2 B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)應用:利用你從(1)選出的等式,完成下列各題:
①已知9x2-4y2=24,3x+2y=6,求3x-2y的值;
②計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲騎自行年,乙乘坐汽車從A地出發沿同一路線勻速前往B地,甲先出發.設甲行駛的時間為x(h),甲、乙兩人距出發點的路程S甲(km)、S乙(km)關于x的函數圖象如圖1所示,甲、乙兩人之同的距離y(km)關于x的函數圖象如圖2所示,請你解決以下問題:
(1)甲的速度是__________km/h,乙的速度是_______km/h;
(2)a=_______,b=_______;
(3)甲出發多少時間后,甲、乙兩人第二次相距7.5km?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com