
【題目】如圖,在平面直角坐標(biāo)系xOy中,雙曲線y=![]() 與直線y=kx﹣2交于點(diǎn)A(3,1).
與直線y=kx﹣2交于點(diǎn)A(3,1).
(1)求直線和雙曲線的解析式;
(2)直線y=kx﹣2與x軸交于點(diǎn)B,點(diǎn)P是雙曲線y=![]() 上一點(diǎn),過點(diǎn)P作直線PC∥x軸,交y軸于點(diǎn)C,交直線y=kx﹣2于點(diǎn)D.若DC=2OB,寫出點(diǎn)P的坐標(biāo).
上一點(diǎn),過點(diǎn)P作直線PC∥x軸,交y軸于點(diǎn)C,交直線y=kx﹣2于點(diǎn)D.若DC=2OB,寫出點(diǎn)P的坐標(biāo).
【答案】解:(1)∵直線y=kx﹣2過點(diǎn)A(3,1),
∴1=3k﹣2.
∴k=1.
∴直線的解析式為y=x﹣2.
∵雙曲線y=![]() 過點(diǎn)A(3,1),
過點(diǎn)A(3,1),
∴m=3.
∴雙曲線的解析式為y=![]() y=
y=![]() .
.
(2)![]() ∵PC∥x軸,DC=2OB,
∵PC∥x軸,DC=2OB,
∴![]()
∴CF=2OF,
由直線y=x﹣2可知F(0,﹣2),
∴OF=2,
∴CF=4,
∴C的坐標(biāo)為(0,2)或(0,﹣6),
∴P的縱坐標(biāo)為2或﹣6,
代入y=![]() 得,2=
得,2=![]() ,解得x=
,解得x=![]() ,
,
﹣6=![]() ,解得x=﹣
,解得x=﹣![]() ,
,
∴P(![]() ,2)或(﹣
,2)或(﹣![]() ,﹣6).
,﹣6).
故答案為P(![]() ,2)或(﹣
,2)或(﹣![]() ,﹣6).
,﹣6).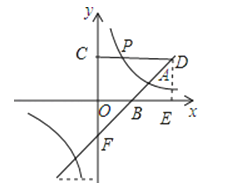
【解析】(1)把A的坐標(biāo)分別代入雙曲線y=![]() 與直線y=kx﹣2,根據(jù)待定系數(shù)法即可求得;
與直線y=kx﹣2,根據(jù)待定系數(shù)法即可求得;
(2)根據(jù)平行線分線段成比例定理得出![]() , 得出CF=2OF,即可求得直線CD與y軸的交點(diǎn)坐標(biāo),從而求得P的縱坐標(biāo),代入(1)求得的解析式即可求得P點(diǎn)的坐標(biāo).
, 得出CF=2OF,即可求得直線CD與y軸的交點(diǎn)坐標(biāo),從而求得P的縱坐標(biāo),代入(1)求得的解析式即可求得P點(diǎn)的坐標(biāo).


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達(dá)標(biāo)測試卷系列答案
芒果教輔達(dá)標(biāo)測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】從-1,1,2這三個(gè)數(shù)字中,隨機(jī)抽取一個(gè)數(shù)記為a,那么,使關(guān)于x的一次函數(shù)y=2x+a的圖象與x軸、y軸圍成的三角形的面積為![]() ,且使關(guān)于x的不等式組
,且使關(guān)于x的不等式組![]() 有解的概率為________.
有解的概率為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
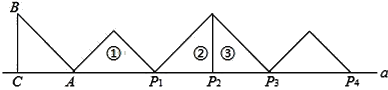
【題目】如圖,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC邊在直線a上,將△ABC繞點(diǎn)A順時(shí)針旋轉(zhuǎn)到位置①可得到點(diǎn)P1,此時(shí)AP1=![]() ;將位置①的三角形繞點(diǎn)P1順時(shí)針旋轉(zhuǎn)到位置②可得到點(diǎn)P2,此時(shí)AP2=
;將位置①的三角形繞點(diǎn)P1順時(shí)針旋轉(zhuǎn)到位置②可得到點(diǎn)P2,此時(shí)AP2=![]() +1;將位置②的三角形繞點(diǎn)P2順時(shí)針旋轉(zhuǎn)到位置③可得到點(diǎn)P3時(shí),AP3=
+1;將位置②的三角形繞點(diǎn)P2順時(shí)針旋轉(zhuǎn)到位置③可得到點(diǎn)P3時(shí),AP3=![]() +2…按此規(guī)律繼續(xù)旋轉(zhuǎn),直至得到點(diǎn)
+2…按此規(guī)律繼續(xù)旋轉(zhuǎn),直至得到點(diǎn)![]() 為止,則
為止,則![]() =________.
=________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】正方形CEDF的頂點(diǎn)D、E、F分別在△ABC的邊AB、BC、AC上.
(1)如圖,若tanB=2,則![]() 的值為
的值為
(2)將△ABC繞點(diǎn)D旋轉(zhuǎn)得到△A′B′C′,連接BB′、CC′.若![]() , 則tanB的值為
, 則tanB的值為 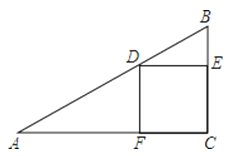
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,定義直線x=m與雙曲線yn=![]() 的交點(diǎn)Am , n(m、n為正整數(shù))為“雙曲格點(diǎn)”,雙曲線yn=
的交點(diǎn)Am , n(m、n為正整數(shù))為“雙曲格點(diǎn)”,雙曲線yn=![]() 在第一象限內(nèi)的部分沿著豎直方向平移或以平行于x軸的直線為對稱軸進(jìn)行翻折之后得到的函數(shù)圖象為其“派生曲線”.
在第一象限內(nèi)的部分沿著豎直方向平移或以平行于x軸的直線為對稱軸進(jìn)行翻折之后得到的函數(shù)圖象為其“派生曲線”.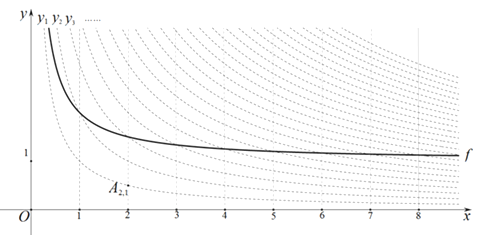
(1)①“雙曲格點(diǎn)”A2 , 1的坐標(biāo)為 ;②若線段A4 , 3A4 , n的長為1個(gè)單位長度,則n= ;
(2)圖中的曲線f是雙曲線y1=![]() 的一條“派生曲線”,且經(jīng)過點(diǎn)A2 , 3 , 則f的解析式為y=
的一條“派生曲線”,且經(jīng)過點(diǎn)A2 , 3 , 則f的解析式為y=
(3)畫出雙曲線y3=![]() 的“派生曲線”g(g與雙曲線y3=
的“派生曲線”g(g與雙曲線y3=![]() 不重合),使其經(jīng)過“雙曲格點(diǎn)”A2 , a、A3 , 3、A4 , b .
不重合),使其經(jīng)過“雙曲格點(diǎn)”A2 , a、A3 , 3、A4 , b .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,已知點(diǎn)A(3,0),B(0,4),將△BOA繞點(diǎn)A按順時(shí)針方向旋轉(zhuǎn)得△CDA,連接OD.當(dāng)∠DOA=∠OBA時(shí),直線CD的解析式為________

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下面是按一定規(guī)律排列且形式相似的一列數(shù):
第1個(gè)數(shù):a1=![]() -(1+
-(1+![]() );
);
第2個(gè)數(shù):a2=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ];
];
第3個(gè)數(shù):a3=![]() -(1+
-(1+![]() )[1+
)[1+![]() ][1+
][1+![]() ][1+
][1+![]() ](1+
](1+![]() ].
].
(1)計(jì)算這三個(gè)數(shù)的結(jié)果(直接寫答案):
a1=___;a2=___;a3=___;
(2)請按上述規(guī)律寫出第4個(gè)數(shù)a4的形式并計(jì)算結(jié)果;
(3)請根據(jù)上述規(guī)律寫出第n (n為正整數(shù))個(gè)數(shù)an的形式(中間部分用省略號,兩端部分必須寫詳細(xì)),然后直接寫出計(jì)算結(jié)果.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
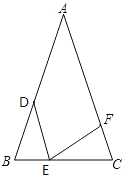
【題目】如圖D、E、F分別在△ABC的三邊上,BD=![]() AB,BE:EC=1:2,AC的長度是FC的3倍,四邊形ADEF的面積是24,則△EFC的面積是_________.
AB,BE:EC=1:2,AC的長度是FC的3倍,四邊形ADEF的面積是24,則△EFC的面積是_________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com