Question

【題目】如圖，已知，和分別平分和，，則的度數為（ ）

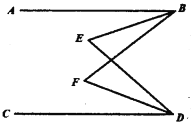
A. 16°B. 32°C. 48°D. 64°

Answer 1

【答案】B

【解析】

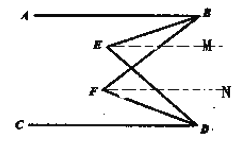
已知BE和DF分別平分∠ABF和∠CDE，根據角平分線分定義可得∠ABE=∠ABF，∠CDF=∠CDE；過點E作EMAB，點F作FNAB，即可得EMFN，由平行線的性質可得∠ABE=∠BEM，∠MED=∠EDC，∠ABF=∠BFN，∠CDF=∠DFN，由此可得∠BED=∠BEM+∠DEM=∠ABE+∠CDE=∠ABF+∠CDE，∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +∠CDE， 又因2∠BED-∠BFD=48°，即可得2（∠ABF+∠CDE）-（∠ABF +∠CDE）=48°，由此即可求得∠CDE=32°.

∵BE和DF分別平分∠ABF和∠CDE，

∴∠ABE=∠ABF，∠CDF=∠CDE，

過點E作EMAB，點F作FNAB，

∵，

∴EMFN，

∴∠ABE=∠BEM，∠MED=∠EDC，∠ABF=∠BFN，∠CDF=∠DFN，

∴∠BED=∠BEM+∠DEM=∠ABE+∠CDE=∠ABF+∠CDE，

∠BFD=∠BFN+∠DFN=∠ABF+∠CDF=∠ABF +∠CDE，

∵2∠BED-∠BFD=48°，

∴2（∠ABF+∠CDE）-（∠ABF +∠CDE）=48°，

∴∠CDE=32°.

故選B.