【題目】在同一平面直角坐標系中，函數y=ax+b與y=ax2﹣bx的圖象可能是（ ）
A．
B．
C．
D．
【答案】C.
【解析】
試題分析：選項A：一次函數圖像經過一、二、三象限，因此a＞0，b＞0，對于二次函數y=ax2﹣bx圖像應該開口向上，對稱軸在y軸右側，不合題意，此選項錯誤；選項B：一次函數圖像經過一、二、四象限，因此a＜0，b＞0，對于二次函數y=ax2﹣bx圖像應該開口向下，對稱軸在y軸左側，不合題意，此選項錯誤；
選項C：一次函數圖像經過一、二、三象限，因此a＞0，b＞0，對于二次函數y=ax2﹣bx圖像應該開口向上，對稱軸在y軸右側，符合題意，此選項正確；選項D：一次函數圖像經過一、二、三象限，因此a＞0，b＞0，對于二次函數y=ax2﹣bx圖像應該開口向上，對稱軸在y軸右側，不合題意，此選項錯誤.故選C.
科目：初中數學 來源： 題型：
【題目】同學們，在我們進入高中以后，將還會學到下面三角函數公式：
sin (α－β)＝sinαcosβ－cosαsinβ，
cos (α－β)＝cosαcosβ＋sinαsinβ
例：sin 15°＝sin (45°－30°)＝sin 45°cos 30°－cos 45°sin 30°＝
(1)試仿照例題，求出cos 15°的準確值；
(2)我們知道，tanα＝
，試求出tan 15°的準確值．
查看答案和解析>>
科目：初中數學 來源： 題型：
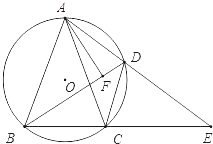
【題目】如圖，△ABC內接于⊙O，且AB＝AC，D是
上一點，AD與BC交于E，AF⊥DB，垂足為F．
（1）求證：∠ADB＝∠CDE；
（2）若AF＝DC＝6，AB＝10，求△DBC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線
與
軸交于點
和點
，與
軸交于點
，連接
交拋物線的對稱軸于點
，
是拋物線的頂點．
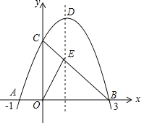
求此拋物線的解析式；
直接寫出點和點的坐標；
若點
在第一象限內的拋物線上，且
，求點坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
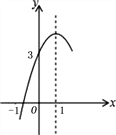
【題目】如圖，拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1，與
軸的一個交點坐標為(－1,0)，其部分圖象如圖所示，下列結論：
① 4ac<b2；② 方程ax2+bx+c=0的兩個根是
；③ 3a+c>0；④ 當y>0時，x的取值范圍是-1≤x<3；⑤ 當x<0時，y隨x增大而增大；
其中結論正確有__________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某超市銷售櫻桃，已知櫻桃的進價為15元/千克，如果售價為20元/千克，那么每天可售出250千克，如果售價為25元/千克，那么每天可獲利2000元，經調查發現：每天的銷售量y（千克）與售價x（元/千克）之間存在一次函數關系．
（1）求y與x之間的函數關系式；
（2）若櫻桃的售價不得高于28元/千克，請問售價定為多少時，該超市每天銷售櫻桃所獲的利潤最大？最大利潤是多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
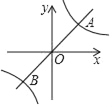
【題目】如圖，一次函數y＝x的圖象與反比例函數y═
的圖象交于A，B兩點，且點A坐標為（1，m）．
（1）求此反比例函數的解析式；
（2）當x取何值時，一次函數大于反比例函數的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
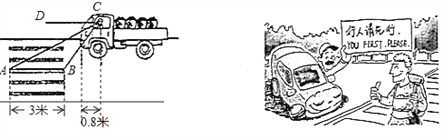
【題目】我國
道路交通安全法
第四十七條規定“機動車行經人行橫道時，應當減速行駛；遇行人通過人行橫道，應當停車讓行” 
如圖：一輛汽車在一個十字路口遇到行人時剎車停下，汽車里的駕駛員看地面的斑馬線前后兩端的視角分別是
和
，如果斑馬線的寬度是
米，駕駛員與車頭的距離是
米，這時汽車車頭與斑馬線的距離x是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC中，∠ACB＝90°，D是邊AB的中點，P是邊AC上一動點，BP與CD相交于點E．
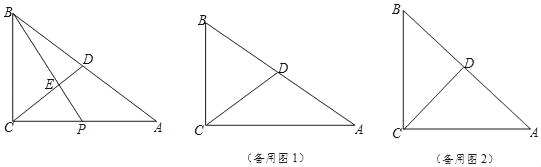
（1）如果BC＝6，AC＝8，且P為AC的中點，求線段BE的長；
（2）聯結PD，如果PD⊥AB，且CE＝2，ED＝3，求cosA的值；
（3）聯結PD，如果BP2＝2CD2，且CE＝2，ED＝3，求線段PD的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com