
【題目】已知![]() ,過點O作
,過點O作![]() .
.
(1)若![]() ,求
,求![]() 的度數;
的度數;
(2)已知射線![]() 平分
平分![]() ,射線
,射線![]() 平分
平分![]() .
.
①若![]() ,求
,求![]() 的度數;
的度數;
②若![]() ,則
,則![]() 的度數為 (直接填寫用含
的度數為 (直接填寫用含![]() 的式子表示的結果).
的式子表示的結果).
【答案】(1)150°或30°;(2)①25°,②![]() θ或180°-
θ或180°-![]() θ
θ
【解析】
(1)分兩種情形畫出圖形求解即可;
(2)①分兩種情形畫出圖形分別求解即可;②分兩種情形分別畫出圖形分別求解即可.
解:(1)如圖1中,∠AOC=∠AOB+∠BOC=150°,
如圖2中,∠AOC=∠BOC-∠AOB=30°.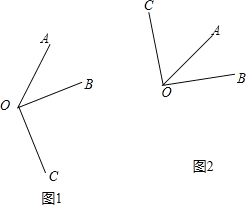
(2)①如圖1-1中,∵∠AOC=∠AOB+∠BOC=140°,
∴∠EOC=![]() ∠AOC=70°,
∠AOC=70°,
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC-∠FOC=25°,
如圖2-1中,∵∠AOC=∠BOC-∠AOB=40°,
∴∠EOC=![]() ∠AOC=20°,
∠AOC=20°,
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠FOC-∠EOC=25°.

②如圖1-2中,∵∠AOC=∠AOB-∠BOC=θ -90°,
∴∠EOC=![]() ∠AOC=
∠AOC=![]() (θ-90°),
(θ-90°),
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC+∠FOC=![]() θ,
θ,
如圖2-2中,∵∠AOC=360°-∠AOB-∠BOC=270°-θ
∴∠EOC=![]() ∠AOC=
∠AOC=![]() (270-θ),
(270-θ),
∵∠FOC=![]() ∠BOC=45°,
∠BOC=45°,
∴∠EOF=∠EOC+∠FOC=180°-![]() θ,
θ,


科目:初中數學 來源: 題型:
【題目】填空,完成下列說理過程
如圖,點A,O,B在同一條直線上,OD,OE分別平分∠AOC和∠BOC.
(1)求∠DOE的度數;
(2)如果∠COD=65°,求∠AOE的度數.

解:(1)如圖,因為OD是∠AOC的平分線,
所以∠COD=![]() ∠AOC.
∠AOC.
因為OE是∠BOC的平分線,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,銳角△ABC內接于⊙O,若⊙O的半徑為6,sinA=![]() ,求BC的長.
,求BC的長.

【答案】BC=8.
【解析】試題分析:通過作輔助線構成直角三角形,再利用三角函數知識進行求解.
試題解析:作⊙O的直徑CD,連接BD,則CD=2×6=12.
∵![]()
∴![]()
∴![]()

點睛:直徑所對的圓周角是直角.
【題型】解答題
【結束】
22
【題目】如圖,一次函數y=k1x+b與反比例函數y=![]() 的圖象交于A(2,m),B(n,﹣2)兩點.過點B作BC⊥x軸,垂足為C,且S△ABC=5.
的圖象交于A(2,m),B(n,﹣2)兩點.過點B作BC⊥x軸,垂足為C,且S△ABC=5.
(1)求一次函數與反比例函數的解析式;
(2)根據所給條件,請直接寫出不等式k1x+b>![]() 的解集;
的解集;
(3)若P(p,y1),Q(﹣2,y2)是函數y=![]() 圖象上的兩點,且y1≥y2,求實數p的取值范圍.
圖象上的兩點,且y1≥y2,求實數p的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,AB=CD,點E、F在BC上,且BF=CE.
(1)求證:△ABE≌△DCF;
(2)試證明:以A、F、D、E為頂點的四邊形是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電視臺的一檔娛樂性節目中,在游戲PK環節,為了隨機分選游戲雙方的組員,主持人設計了以下游戲:用不透明的白布包住三根顏色長短相同的細繩AA1、BB1、CC1,只露出它們的頭和尾(如圖所示),由甲、乙兩位嘉賓分別從白布兩端各選一根細繩,并拉出,若兩人選中同一根細繩,則兩人同隊,否則互為反方隊員.
(1)若甲嘉賓從中任意選擇一根細繩拉出,求他恰好抽出細繩AA1的概率;
(2)請用畫樹狀圖法或列表法,求甲、乙兩位嘉賓能分為同隊的概率.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平面直角坐標系中兩定點A(﹣1,0)、B(4,0),拋物線y=ax2+bx﹣2(a≠0)過點A,B,頂點為C,點P(m,n)(n<0)為拋物線上一點.
(1)求拋物線的解析式和頂點C的坐標;
(2)當∠APB為鈍角時,求m的取值范圍;
(3)若m>![]() ,當∠APB為直角時,將該拋物線向左或向右平移t(0<t<
,當∠APB為直角時,將該拋物線向左或向右平移t(0<t<![]() )個單位,點C、P平移后對應的點分別記為C′、P′,是否存在t,使得首位依次連接A、B、P′、C′所構成的多邊形的周長最短?若存在,求t的值并說明拋物線平移的方向;若不存在,請說明理由.
)個單位,點C、P平移后對應的點分別記為C′、P′,是否存在t,使得首位依次連接A、B、P′、C′所構成的多邊形的周長最短?若存在,求t的值并說明拋物線平移的方向;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下列語句畫圖:
(1)畫∠AOB=120°;
(2)畫∠AOB的角平分線OC;
(3)反向延長OC得射線OD;
(4)分別在射線OA、OB、OD上畫線段OE=OF=OG=2cm;
(5)連接EF、EG、FG;
(6)你能發現EF、EG、FG有什么關系?∠EFG、∠EGF、∠GEF有什么關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數 y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸是直線 x=1,下列結論:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正確的是_____.
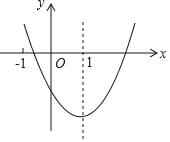
查看答案和解析>>
科目:初中數學 來源: 題型:
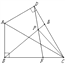
【題目】如圖,在Rt△ABC中,∠ABC=90°,∠ACB=30°,BC=2![]() ,△ADC與△ABC關于AC對
,△ADC與△ABC關于AC對
稱,點E、F分別是邊DC、BC上的任意一點,且DE=CF,BE、DF相交于點P,則CP的最小值為( )
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com