
【題目】問題提出
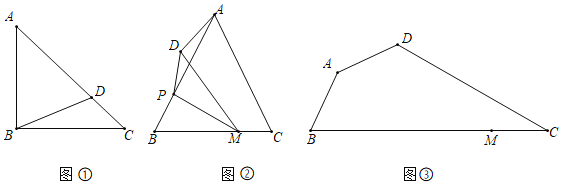
(1)如圖①,在等腰Rt△ABC中,斜邊AC=4,點(diǎn)D為AC上一點(diǎn),連接BD,則BD的最小值為 ;
問題探究
(2)如圖②,在△ABC中,AB=AC=5,BC=6,點(diǎn)M是BC上一點(diǎn),且BM=4,點(diǎn)P是邊AB上一動(dòng)點(diǎn),連接PM,將△BPM沿PM翻折得到△DPM,點(diǎn)D與點(diǎn)B對(duì)應(yīng),連接AD,求AD的最小值;
問題解決
(3)如圖③,四邊形ABCD是規(guī)劃中的休閑廣場(chǎng)示意圖,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2![]() km,AB=3km,點(diǎn)M是BC上一點(diǎn),MC=4km.現(xiàn)計(jì)劃在四邊形ABCD內(nèi)選取一點(diǎn)P,把△DCP建成商業(yè)活動(dòng)區(qū),其余部分建成景觀綠化區(qū).為方便進(jìn)入商業(yè)區(qū),需修建小路BP、MP,從實(shí)用和美觀的角度,要求滿足∠PMB=∠ABP,且景觀綠化區(qū)面積足夠大,即△DCP區(qū)域面積盡可能小.則在四邊形ABCD內(nèi)是否存在這樣的點(diǎn)P?若存在,請(qǐng)求出△DCP面積的最小值;若不存在,請(qǐng)說明理由.
km,AB=3km,點(diǎn)M是BC上一點(diǎn),MC=4km.現(xiàn)計(jì)劃在四邊形ABCD內(nèi)選取一點(diǎn)P,把△DCP建成商業(yè)活動(dòng)區(qū),其余部分建成景觀綠化區(qū).為方便進(jìn)入商業(yè)區(qū),需修建小路BP、MP,從實(shí)用和美觀的角度,要求滿足∠PMB=∠ABP,且景觀綠化區(qū)面積足夠大,即△DCP區(qū)域面積盡可能小.則在四邊形ABCD內(nèi)是否存在這樣的點(diǎn)P?若存在,請(qǐng)求出△DCP面積的最小值;若不存在,請(qǐng)說明理由.
【答案】(1)2;(2)![]() ;(3) 存在點(diǎn)P,使得△DCP的面積最小,△DCP面積的最小值是(
;(3) 存在點(diǎn)P,使得△DCP的面積最小,△DCP面積的最小值是(![]() ﹣20)km2.
﹣20)km2.
【解析】
(1)如圖1,當(dāng)BD⊥AC時(shí),BD的值最小,根據(jù)直角三角形斜邊中線的性質(zhì)可得結(jié)論;
(2)如圖2,根據(jù)BM=DM可知:點(diǎn)D在以M為圓心,BM為半徑的⊙M上,連接AM交⊙M于點(diǎn)D',此時(shí)AD值最小,計(jì)算AM和半徑D'M的長(zhǎng),可得AD的最小值;
(3)如圖3,先確定點(diǎn)P的位置,再求△DCP的面積;假設(shè)在四邊形ABCD中存在點(diǎn)P,以BM為邊向下作等邊△BMF,可知:A、F、M、P四點(diǎn)共圓,作△BMF的外接圓⊙O,圓外一點(diǎn)與圓心的連線的交點(diǎn)就是點(diǎn)P的位置,并構(gòu)建直角三角形,計(jì)算CD和PQ的長(zhǎng),由三角形的面積公式可求得面積.
解:(1)當(dāng)BD⊥AC時(shí),如圖1,

∵AB=BC,
∴D是AC的中點(diǎn),
∴BD=![]() AC=
AC=![]() ×4=2,即BD的最小值是2;
×4=2,即BD的最小值是2;
故答案為2;
(2)如圖2,由題意得:DM=MB,
∴點(diǎn)D在以M為圓心,BM為半徑的⊙M上,連接AM交⊙M于點(diǎn)D',此時(shí)AD值最小,
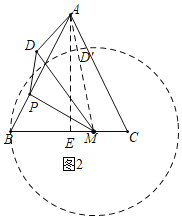
過A作AE⊥BC于E,
∵AB=AC=5,
∴BE=EC=![]() BC=
BC=![]() ,
,
由勾股定理得:AE=![]() 4,
4,
∵BM=4,
∴EM=4﹣3=1,
∴AM=![]() ,
,
∵D'M=BM=4,
∴AD'=AM﹣D'M=![]() ﹣4,
﹣4,
即線段AD長(zhǎng)的最小值是![]() ﹣4;
﹣4;
(3)如圖3,假設(shè)在四邊形ABCD中存在點(diǎn)P,
∵∠BAD=∠ADC=135°,∠DCB=30°,
∴∠ABC=360°﹣∠BAD﹣∠ADC﹣∠DCB=60°,
∵∠PMB=∠ABP,
∴∠BPM=180°﹣∠PBM﹣∠PMB=180°﹣(∠PBM+∠ABP)=180°﹣∠ABC=120°,
以BM為邊向下作等邊△BMF,作△BMF的外接圓⊙O,

∵∠BFM+∠BPM=60°+120°=180°,則點(diǎn)P在![]() 上,
上,
過O作OQ⊥CD于Q,交⊙O于點(diǎn)P,
設(shè)點(diǎn)P'是![]() 上任意一點(diǎn),連接OP',過P'作P'H⊥CD于H,
上任意一點(diǎn),連接OP',過P'作P'H⊥CD于H,
可得OP'+P'H≥OQ=OP+PQ,即P'H≥PQ,
∴P即為所求的位置,
延長(zhǎng)CD,BA交于點(diǎn)E,
∵∠BAD=∠ADC=135°,∠DCB=30°,∠ABC=60°,
∴∠E=90°,∠EAD=∠EDA=45°,
∵AD=2![]() ,
,
∴AE=DE=2,
∴BE=AE+AB=5,BC=2BE=10,CE=5![]() ,
,
∴BM=BC﹣MC=6,CD=5![]() ﹣2,
﹣2,
過O作OG⊥BM于G,
∵∠BOM=2∠BFM=120°,OB=OM,
∴∠OBM=30°,
∴∠ABO=∠ABM+∠MBO=90°,OB![]() =2
=2![]() ,
,
∴∠E=∠ABO=∠OQE=90°,
∴四邊形OBEQ是矩形,
∴OQ=BE=5,
∴PQ=OQ﹣OP=5﹣2![]() ,
,
∴S△DPC=![]() ﹣20,
﹣20,
∴存在點(diǎn)P,使得△DCP的面積最小,△DCP面積的最小值是(![]() ﹣20)km2.
﹣20)km2.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】據(jù)報(bào)載,在“百萬家庭低碳行,垃圾分類要先行”活動(dòng)中,某地區(qū)對(duì)隨機(jī)抽取的1000名公民的年齡段分布情況和對(duì)垃圾分類所持態(tài)度進(jìn)行調(diào)查,并將調(diào)查結(jié)果分別繪成條形圖(圖1)、扇形圖(圖2).
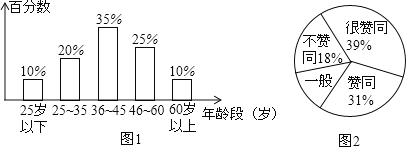
(1)圖2中所缺少的百分?jǐn)?shù)是_________;
(2)這次隨機(jī)調(diào)查中,如果公民年齡的中位數(shù)是正整數(shù),那么這個(gè)中位數(shù)所在年齡段是_________(填寫年齡段);
(3)這次隨機(jī)調(diào)查中,年齡段是“25歲以下”的公民中“不贊成”的有5名,它占“25歲以下”人數(shù)的百分?jǐn)?shù)是________;
(4)如果把所持態(tài)度中的“很贊同”和“贊同”統(tǒng)稱為“支持”,那么這次被調(diào)查公民中“支持”的人有_______名.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)),與
的左側(cè)),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,對(duì)稱軸與
,對(duì)稱軸與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在拋物線上.
在拋物線上.
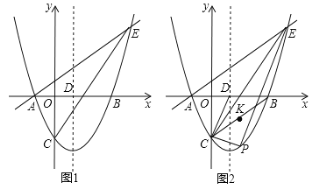
(1)求直線![]() 的解析式.
的解析式.
(2)點(diǎn)![]() 為直線
為直線![]() 下方拋物線上的一點(diǎn),連接
下方拋物線上的一點(diǎn),連接![]() ,
,![]() .當(dāng)
.當(dāng)![]() 的面積最大時(shí),連接
的面積最大時(shí),連接![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是線段
是線段![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是線段
是線段![]() 上的一點(diǎn),點(diǎn)
上的一點(diǎn),點(diǎn)![]() 是線段
是線段![]() 上的一點(diǎn),求
上的一點(diǎn),求![]() 的最小值.
的最小值.
(3)點(diǎn)![]() 是線段
是線段![]() 的中點(diǎn),將拋物線
的中點(diǎn),將拋物線![]() 與
與![]() 軸正方向平移得到新拋物線
軸正方向平移得到新拋物線![]() ,
,![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,
,![]() 的頂點(diǎn)為點(diǎn)
的頂點(diǎn)為點(diǎn)![]() ,在新拋物線
,在新拋物線![]() 的對(duì)稱軸上,是否存在點(diǎn)
的對(duì)稱軸上,是否存在點(diǎn)![]() ,使得
,使得![]() 為等腰三角形?若存在,直接寫出點(diǎn)
為等腰三角形?若存在,直接寫出點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說明理由.
的坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為實(shí)現(xiàn)2020年全面脫貧的目標(biāo),我國(guó)實(shí)施“精準(zhǔn)扶貧”戰(zhàn)略,從而使貧困戶的生活條件得到改善,生活質(zhì)量明顯提高.為了切實(shí)關(guān)注、關(guān)愛貧困家庭學(xué)生,某校對(duì)全校各班貧困家庭學(xué)生的人數(shù)情況進(jìn)行了統(tǒng)計(jì),統(tǒng)計(jì)發(fā)現(xiàn)班上貧困家庭學(xué)生人數(shù)分別有2名,3名,4名,5名,6名,共五種情況.并將其制成了如下兩幅不完整的統(tǒng)計(jì)圖:

請(qǐng)回答下列問題:
(1)求該校一共有班級(jí)________個(gè);在扇形統(tǒng)計(jì)圖中,貧困家庭學(xué)生人數(shù)有5名的班級(jí)所對(duì)應(yīng)扇形圓心角為________°;
(2)將條形圖補(bǔ)充完整;
(3)甲、乙、丙是貧困生中的三名學(xué)生,學(xué)校決定從這三名學(xué)生中隨機(jī)抽取兩名代表到市里進(jìn)行發(fā)言,用列表法或畫樹狀圖法,求同時(shí)抽到甲,乙兩名學(xué)生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】漢江是長(zhǎng)江最長(zhǎng)的支流,在歷史上占居重要地位,陜西省境內(nèi)的漢江為漢江上游段.李琳利用熱氣球探測(cè)器測(cè)量漢江某段河寬,如圖,探測(cè)器在A處觀測(cè)到正前方漢江兩岸岸邊的B、C兩點(diǎn),并測(cè)得B、C兩點(diǎn)的俯角分別為45°,30°已知A處離地面的高度為80m,河平面BC與地面在同一水平面上,請(qǐng)你求出漢江該段河寬BC.(結(jié)果保留根號(hào))
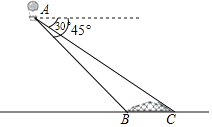
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某劇院舉行專場(chǎng)音樂會(huì),成人票每張20元,學(xué)生票每張5元. 暑假期間,為了豐富廣大師生的業(yè)余文化生活,影劇院制定了兩種優(yōu)惠方案,方案一:購(gòu)買一張成人票贈(zèng)送一張學(xué)生票;方案二:按總價(jià)的90%付款. 某校有4名老師帶隊(duì),與若干名(不少于4人)學(xué)生一起聽音樂會(huì).設(shè)學(xué)生人數(shù)為![]() 人,
人,![]() (
(![]() 為整數(shù)).
為整數(shù)).
(1)根據(jù)題意填表:
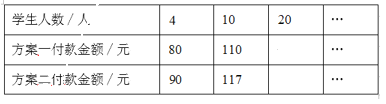
(2)設(shè)方案一付款總金額為![]() 元,方案二付款總金額為
元,方案二付款總金額為![]() 元,分別求
元,分別求![]() ,
,![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(3)根據(jù)題意填空:
①若用兩種方案購(gòu)買音樂會(huì)的花費(fèi)相同,則聽音樂會(huì)的學(xué)生有 人;
②若有60名學(xué)生聽音樂會(huì),則用方案 購(gòu)買音樂會(huì)票的花費(fèi)少;
③若用一種方案購(gòu)買音樂會(huì)票共花費(fèi)了![]() 元,則用方案 購(gòu)買音樂會(huì)票,使聽音樂的學(xué)生人數(shù)多.
元,則用方案 購(gòu)買音樂會(huì)票,使聽音樂的學(xué)生人數(shù)多.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,點(diǎn)![]() ,
,![]() 在反比例函數(shù)圖象上,作直線
在反比例函數(shù)圖象上,作直線![]() ,連接
,連接![]() 、
、![]() .
.
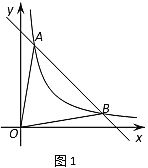
(1)求反比例函數(shù)的表達(dá)式和![]() 的值;
的值;
(2)求![]() 的面積;
的面積;
(3)如圖2,![]() 是線段
是線段![]() 上一點(diǎn),作
上一點(diǎn),作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸的垂線,交反比例函數(shù)圖象于點(diǎn)
軸的垂線,交反比例函數(shù)圖象于點(diǎn)![]() ,若
,若![]() ,求出點(diǎn)
,求出點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
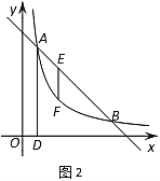
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 為
為![]() 的直徑,
的直徑,![]() 為
為![]() 的切線,
的切線,![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 為弧
為弧![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() .
.
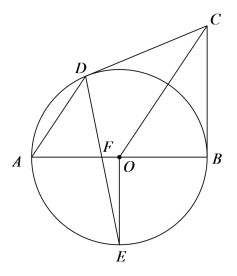
(1)求證:![]() 為
為![]() 的切線;
的切線;
(2)求證:![]() ;
;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明在研究拋物線![]() (
(![]() 為常數(shù))時(shí),得到如下結(jié)論,其中正確的是( )
為常數(shù))時(shí),得到如下結(jié)論,其中正確的是( )
A.無論![]() 取何實(shí)數(shù),
取何實(shí)數(shù),![]() 的值都小于0
的值都小于0
B.該拋物線的頂點(diǎn)始終在直線![]() 上
上
C.當(dāng)![]() 時(shí),
時(shí),![]() 隨
隨![]() 的增大而增大,則
的增大而增大,則![]()
D.該拋物線上有兩點(diǎn)![]() ,
,![]() ,若
,若![]() ,
,![]() ,則
,則![]()
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com