
【題目】我們定義:兩個二次項系數(shù)之和為1,對稱軸相同,且圖象與y軸交點(diǎn)也相同的二次函數(shù)互為友好同軸二次函數(shù)![]() 例如:
例如:![]() 的友好同軸二次函數(shù)為
的友好同軸二次函數(shù)為![]() .
.
![]() 請你分別寫出
請你分別寫出![]() ,
,![]() 的友好同軸二次函數(shù);
的友好同軸二次函數(shù);
![]() 滿足什么條件的二次函數(shù)沒有友好同軸二次函數(shù)?滿足什么條件的二次函數(shù)的友好同軸二次函數(shù)是它本身?
滿足什么條件的二次函數(shù)沒有友好同軸二次函數(shù)?滿足什么條件的二次函數(shù)的友好同軸二次函數(shù)是它本身?
![]() 如圖,二次函數(shù)
如圖,二次函數(shù)![]() :
:![]() 與其友好同軸二次函數(shù)
與其友好同軸二次函數(shù)![]() 都與y軸交于點(diǎn)A,點(diǎn)B、C分別在
都與y軸交于點(diǎn)A,點(diǎn)B、C分別在![]() 、
、![]() 上,點(diǎn)B,C的橫坐標(biāo)均為
上,點(diǎn)B,C的橫坐標(biāo)均為![]() ,它們關(guān)于
,它們關(guān)于![]() 的對稱軸的對稱點(diǎn)分別為
的對稱軸的對稱點(diǎn)分別為![]() ,
,![]() ,連結(jié)
,連結(jié)![]() ,
,![]() ,
,![]() ,CB.
,CB.
![]() 若
若![]() ,且四邊形
,且四邊形![]() 為正方形,求m的值;
為正方形,求m的值;
![]() 若
若![]() ,且四邊形
,且四邊形![]() 的鄰邊之比為1:2,直接寫出a的值.
的鄰邊之比為1:2,直接寫出a的值.
【答案】![]() 函數(shù)
函數(shù)![]() 的友好同軸二次函數(shù)為
的友好同軸二次函數(shù)為![]() ;函數(shù)
;函數(shù)![]() 的友好同軸二次函數(shù)為
的友好同軸二次函數(shù)為![]() ;
;![]() 二次項系數(shù)為1的二次函數(shù)沒有友好同軸二次函數(shù);二次項系數(shù)為
二次項系數(shù)為1的二次函數(shù)沒有友好同軸二次函數(shù);二次項系數(shù)為![]() 的二次函數(shù)的友好同軸二次函數(shù)是它本身;
的二次函數(shù)的友好同軸二次函數(shù)是它本身;![]() 的值為
的值為![]() ;
;![]() 的值為
的值為![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)根據(jù)友好同軸二次函數(shù)的定義,找出![]() 、
、![]() 的友好同軸二次函數(shù)即可;
的友好同軸二次函數(shù)即可;
(2)由二次項系數(shù)非零可得出二次項系數(shù)為1的二次函數(shù)沒有友好同軸二次函數(shù),由友好同軸二次函數(shù)的定義可知:二次項系數(shù)為![]() 的二次函數(shù)的友好同軸二次函數(shù)是它本身;
的二次函數(shù)的友好同軸二次函數(shù)是它本身;
(3)根據(jù)二次函數(shù)L_1的解析式找出其友好同軸二次函數(shù)L_2的函數(shù)解析式.
①代入a=3,利用二次函數(shù)圖象上點(diǎn)的坐標(biāo)特征可得出點(diǎn)B、C、B'、C'的坐標(biāo),進(jìn)而可得出BC、BB'的值,由正方形的性質(zhì)可得出BC=BB',即關(guān)于m的一元二次方程,解之取其大于0小于2的值即可得出結(jié)論;
②由m=1,利用二次函數(shù)圖象上點(diǎn)的坐標(biāo)特征可得出點(diǎn)B、C、B'、C'的坐標(biāo),進(jìn)而可得出BC、BB'的值,由兩邊之比為1:2,即可得出關(guān)于a的含絕對值符號的一元一次方程,解之即可得出結(jié)論.
![]() ,
,
![]() 函數(shù)
函數(shù)![]() 的友好同軸二次函數(shù)為
的友好同軸二次函數(shù)為![]() ;
;
![]() ,
,![]() ,
,
![]() 函數(shù)
函數(shù)![]() 的友好同軸二次函數(shù)為
的友好同軸二次函數(shù)為![]() .
.
![]() ,
,
![]() 二次項系數(shù)為1的二次函數(shù)沒有友好同軸二次函數(shù);
二次項系數(shù)為1的二次函數(shù)沒有友好同軸二次函數(shù);
![]() ,
,
![]() 二次項系數(shù)為
二次項系數(shù)為![]() 的二次函數(shù)的友好同軸二次函數(shù)是它本身.
的二次函數(shù)的友好同軸二次函數(shù)是它本身.
![]() 二次函數(shù)
二次函數(shù)![]() :
:![]() 的對稱軸為直線
的對稱軸為直線![]() ,其友好同軸二次函數(shù)
,其友好同軸二次函數(shù)![]() :
:![]() .
.
![]() ,
,
![]() 二次函數(shù)
二次函數(shù)![]() :
:![]() ,二次函數(shù)
,二次函數(shù)![]() :
:![]() ,
,
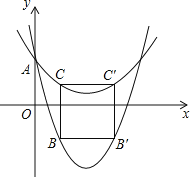
![]() 點(diǎn)B的坐標(biāo)為
點(diǎn)B的坐標(biāo)為![]() ,點(diǎn)C的坐標(biāo)為
,點(diǎn)C的坐標(biāo)為![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
![]() ,
,![]() .
.
![]() 四邊形
四邊形![]() 為正方形,
為正方形,
![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() 不合題意,舍去
不合題意,舍去![]() ,
,
![]() 的值為
的值為![]() .
.
![]() 當(dāng)
當(dāng)![]() 時,點(diǎn)B的坐標(biāo)為
時,點(diǎn)B的坐標(biāo)為![]() ,點(diǎn)C的坐標(biāo)為
,點(diǎn)C的坐標(biāo)為![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
![]() ,
,![]() .
.
![]() 四邊形
四邊形![]() 的鄰邊之比為1:2,
的鄰邊之比為1:2,
![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 的值為
的值為![]() 、
、![]() 、
、![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為決定誰獲得僅有的一張電影票,甲和乙設(shè)計了如下游戲:在三張完全相同的卡片上,分別寫上字母![]() ,
,![]() ,
,![]() ,背面朝上,每次活動洗均勻.
,背面朝上,每次活動洗均勻.
甲說:我隨機(jī)抽取一張,若抽到字母![]() ,電影票歸我;
,電影票歸我;
乙說:我隨機(jī)抽取一張后放回,再隨機(jī)抽取一張,若兩次抽取的字母相同的電影票歸我.
![]() 求甲獲得電影票的概率;
求甲獲得電影票的概率;![]() 求乙獲得電影票的概率;
求乙獲得電影票的概率;![]() 此游戲?qū)φl有利?
此游戲?qū)φl有利?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如果一個分式的分子或分母可以因式分解,且這個分式不可約分,那么我們稱這
個分式為“和諧分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④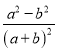 . 其中是“和諧分式”是 (填寫序號即可);
. 其中是“和諧分式”是 (填寫序號即可);
(2)若![]() 為正整數(shù),且
為正整數(shù),且![]() 為“和諧分式”,請寫出
為“和諧分式”,請寫出![]() 的值;
的值;
(3)在化簡![]() 時,
時,
小東和小強(qiáng)分別進(jìn)行了如下三步變形:
小東: ![]()
![]()

小強(qiáng): ![]()
![]()
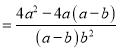
顯然,小強(qiáng)利用了其中的和諧分式, 第三步所得結(jié)果比小東的結(jié)果簡單,
原因是: ,
請你接著小強(qiáng)的方法完成化簡.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩車同時從![]() 城出發(fā)駛向
城出發(fā)駛向![]() 城,甲車到達(dá)
城,甲車到達(dá)![]() 城后立即返回.如圖它們離
城后立即返回.如圖它們離![]() 城的距離
城的距離![]() (千米)與行駛時間
(千米)與行駛時間![]() (小時)之間的函數(shù)圖象.
(小時)之間的函數(shù)圖象.
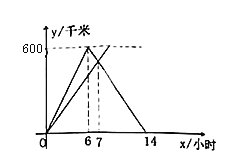
(1)求甲車行駛過程中![]() 與
與![]() 的函數(shù)解析式,并寫出自變量
的函數(shù)解析式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)求相遇時間和乙車速度;
(3)在什么時間段內(nèi)甲車在乙車前面?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,拋物線C1:y=ax2﹣2ax+c(a<0)與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C.已知點(diǎn)A的坐標(biāo)為(﹣1,0),點(diǎn)O為坐標(biāo)原點(diǎn),OC=3OA,拋物線C1的頂點(diǎn)為G.
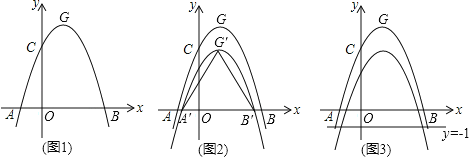
(1)求出拋物線C1的解析式,并寫出點(diǎn)G的坐標(biāo);
(2)如圖2,將拋物線C1向下平移k(k>0)個單位,得到拋物線C2,設(shè)C2與x軸的交點(diǎn)為A′、B′,頂點(diǎn)為G′,當(dāng)△A′B′G′是等邊三角形時,求k的值:
(3)在(2)的條件下,如圖3,設(shè)點(diǎn)M為x軸正半軸上一動點(diǎn),過點(diǎn)M作x軸的垂線分別交拋物線C1、C2于P、Q兩點(diǎn),試探究在直線y=﹣1上是否存在點(diǎn)N,使得以P、Q、N為頂點(diǎn)的三角形與△AOQ全等,若存在,直接寫出點(diǎn)M,N的坐標(biāo):若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)y=ax2+2x+c的圖象經(jīng)過點(diǎn)C(0,3),與x軸分別交于點(diǎn)A,點(diǎn)B(3,0).點(diǎn)P是直線BC上方的拋物線上一動點(diǎn).
(1)求二次函數(shù)y=ax2+2x+c的表達(dá)式;
(2)連接PO,PC,并把△POC沿y軸翻折,得到四邊形POP′C.若四邊形POP′C為菱形,請求出此時點(diǎn)P的坐標(biāo);
(3)當(dāng)點(diǎn)P運(yùn)動到什么位置時,四邊形ACPB的面積最大?求出此時P點(diǎn)的坐標(biāo)和四邊形ACPB的最大面積.
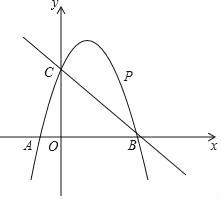
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() ,
,![]() 是
是![]() 上的一點(diǎn),
上的一點(diǎn),![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 上的一動點(diǎn),點(diǎn)
上的一動點(diǎn),點(diǎn)![]() 為
為![]() 上的一動點(diǎn),則
上的一動點(diǎn),則![]() 的最小值為 ________,當(dāng)
的最小值為 ________,當(dāng)![]() 的值取最小值時,則
的值取最小值時,則![]() 的面積為________.
的面積為________.
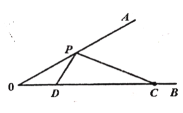
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,將
,將![]() 繞著點(diǎn)
繞著點(diǎn)![]() 旋轉(zhuǎn)
旋轉(zhuǎn)![]() 后得到
后得到![]() .
.
![]() 在圖中畫出
在圖中畫出![]() ;
;
![]() 點(diǎn)
點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的對應(yīng)點(diǎn)
的對應(yīng)點(diǎn)![]() ’和
’和![]() ’的坐標(biāo)分別是
’的坐標(biāo)分別是![]() ’________和
’________和![]() ’________;
’________;
![]() 請直接寫出
請直接寫出![]() 和
和![]() ’
’![]() ’的數(shù)量關(guān)系和位置關(guān)系.
’的數(shù)量關(guān)系和位置關(guān)系.
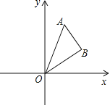
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某民俗旅游村為接待游客住宿需要,開設(shè)了有![]() 張床位的旅館,當(dāng)每張床位每天收費(fèi)
張床位的旅館,當(dāng)每張床位每天收費(fèi)![]() 元時,床位可全部租出.若每張床位每天收費(fèi)提高
元時,床位可全部租出.若每張床位每天收費(fèi)提高![]() 元,則相應(yīng)的減少了
元,則相應(yīng)的減少了![]() 張床位租出.如果每張床位每天以
張床位租出.如果每張床位每天以![]() 元為單位提高收費(fèi),為使租出的床位少且租金高,那么每張床位每天最合適的收費(fèi)是( )
元為單位提高收費(fèi),為使租出的床位少且租金高,那么每張床位每天最合適的收費(fèi)是( )
A. 14元 B. 15元 C. 16元 D. 18元
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com