
如圖,已知拋物線 (b,c是常數,且c<0)與x軸分別交于點A,B(點A位于點B的左側),與y軸的負半軸交于點C,點A的坐標為(-1,0).
(b,c是常數,且c<0)與x軸分別交于點A,B(點A位于點B的左側),與y軸的負半軸交于點C,點A的坐標為(-1,0).

(1)b= ,點B的橫坐標為 (上述結果均用含c的代數式表示);
(2)連接BC,過點A作直線AE∥BC,與拋物線 交于點E.點D是x軸上一點,其坐標為
交于點E.點D是x軸上一點,其坐標為
(2,0),當C,D,E三點在同一直線上時,求拋物線的解析式;
(3)在(2)的條件下,點P是x軸下方的拋物線上的一動點,連接PB,PC,設所得△PBC的面積為S.
①求S的取值范圍;
②若△PBC的面積S為整數,則這樣的△PBC共有 個.
解:(1)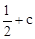 ;
;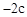 。
。
(2)在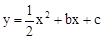 中,令x=0,得y=c,
中,令x=0,得y=c,
∴點C的坐標為(c,0)。
設直線BC的解析式為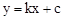 ,
,
∵點B的坐標為(-2 c,0),∴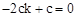 。
。
∵ ,∴
,∴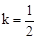 。
。
∴直線BC的解析式為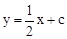 。
。
∵AE∥BC,∴可設直線AE的解析式為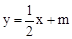 。
。
∵點A的坐標為(-1,0),∴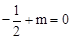 ,
,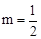 。
。
∴直線AE的解析式為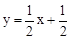 。
。
由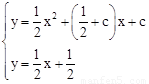 解得
解得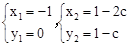 。
。
∴點E的坐標為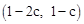 。
。
∵點C的坐標為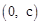 ,點D的坐標為(2,0),∴直線CD的解析式為
,點D的坐標為(2,0),∴直線CD的解析式為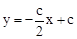 。
。
∵點C,D,E三點在同一直線上,∴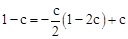 。
。
∴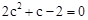 ,解得
,解得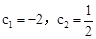 (舍去)。
(舍去)。
∴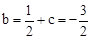 。
。
∴拋物線的解析式為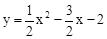 。
。
(3)①設點P的坐標為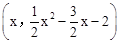 ,
,
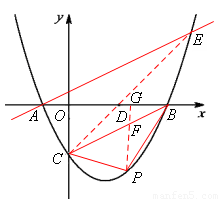
∵點A的坐標為(-1,0),點B的坐標為(4,0),點C的坐標為(0,-2),
∴AB=5,OC=2,直線CB的解析式為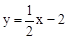 。
。
當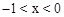 時,
時,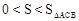 ,
,
∵ ,∴
,∴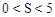 。
。
當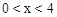 時,過點P作PG⊥x軸于點G,交BC于點F,
時,過點P作PG⊥x軸于點G,交BC于點F,
∴點F的坐標為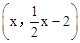 。
。
∴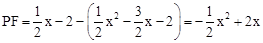 。
。
∴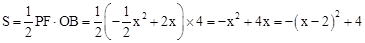 。
。
∴當x=2時, 。∴
。∴
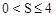 。
。
綜上所述,S的取值范圍為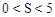 。
。
②11。
【解析】
試題分析:(1)將點A的坐標為(-1,0)代入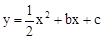 得
得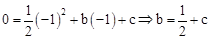 。
。
∴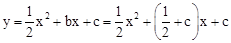 。
。
令 ,解得
,解得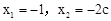 。
。
∴點B的橫坐標為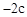 。
。
(2)求出直線BC的解析式,從而求出直線AE的解析式,得到點E的坐標為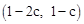 ,由點C,D,E三點在同一直線上,將
,由點C,D,E三點在同一直線上,將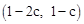 代入直線CD的解析式
代入直線CD的解析式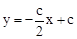 即可求出c,由(1)
即可求出c,由(1)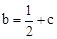 求出b,從而得到拋物線的解析式。
求出b,從而得到拋物線的解析式。
(3)①分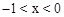 和
和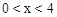 兩種情況討論。
兩種情況討論。
②當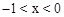 時,
時,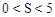 ,且S為整數,對應的x有4個;
,且S為整數,對應的x有4個;
當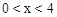 時,
時,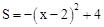 ,
,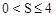 ,且S為整數,對應的x有7個(
,且S為整數,對應的x有7個(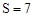 時只有1個)。
時只有1個)。
∴若△PBC的面積S為整數,則這樣的△PBC共有11個。


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
 C(0,3).
C(0,3).查看答案和解析>>
科目:初中數學 來源: 題型:
 、C(0,-3)兩點,與x軸交于另一點B.
、C(0,-3)兩點,與x軸交于另一點B.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•衡陽)如圖,已知拋物線經過A(1,0),B(0,3)兩點,對稱軸是x=-1.
(2013•衡陽)如圖,已知拋物線經過A(1,0),B(0,3)兩點,對稱軸是x=-1.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1,且拋物線經過A(-1,0)、C(0,-3)兩點,與x軸交于另一點B.
如圖,已知拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=1,且拋物線經過A(-1,0)、C(0,-3)兩點,與x軸交于另一點B.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知拋物線y=ax2+bx+c的頂點是(-1,-4),且與x軸交于A、B(1,0)兩點,交y軸于點C;
如圖,已知拋物線y=ax2+bx+c的頂點是(-1,-4),且與x軸交于A、B(1,0)兩點,交y軸于點C;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com