
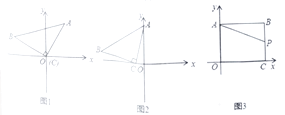
【題目】(1)操作思考:如圖1,在平面直角坐標系中,等腰直角![]() 的直角頂點
的直角頂點![]() 在原點,將其繞著點
在原點,將其繞著點![]() 旋轉,若頂點
旋轉,若頂點![]() 恰好落在點
恰好落在點![]() 處.則①
處.則①![]() 的長為______;②點
的長為______;②點![]() 的坐標為______(直接寫結果)
的坐標為______(直接寫結果)
(2)感悟應用:如圖2,在平面直角坐標系中,將等腰直角![]() 如圖放置,直角頂點
如圖放置,直角頂點![]() ,點
,點![]() ,試求直線
,試求直線![]() 的函數表達式.
的函數表達式.
(3)拓展研究:如圖3,在直角坐標系中,點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,作
,作![]() 軸,垂足為點
軸,垂足為點![]() 是線段
是線段![]() 上的一個動點,點
上的一個動點,點![]() 是直線
是直線![]() 上一動點.問是否存在以點
上一動點.問是否存在以點![]() 為直角頂點的等腰直角
為直角頂點的等腰直角![]() ,若存在,請直接寫出此時
,若存在,請直接寫出此時![]() 點的坐標,若不存在,請說明理由.
點的坐標,若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據勾股定理可得OA長,由![]() 對應邊相等可得B點坐標;
對應邊相等可得B點坐標;
(2)通過證明![]() 得出點B坐標,用待定系數法求直線
得出點B坐標,用待定系數法求直線![]() 的函數表達式;
的函數表達式;
(3)設點Q坐標為![]() ,可通過證三角形全等的性質可得a的值,由Q點坐標可間接求出P點坐標.
,可通過證三角形全等的性質可得a的值,由Q點坐標可間接求出P點坐標.
解:(1)如圖1,作![]() 軸于F,
軸于F,![]() 軸于E.
軸于E.
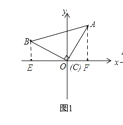
由A點坐標可知![]()
在![]() 中,根據勾股定理可得
中,根據勾股定理可得![]() ;
;
![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]()
![]() 軸于F,
軸于F,![]() 軸于E
軸于E
![]()
又![]()
![]()
![]()
![]()
所以B點坐標為:![]()
(2)如圖,過點![]() 作
作![]() 軸.
軸.
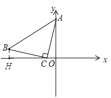
![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]()
![]() 軸
軸
![]()
又![]()
![]()
∴![]() ,
,
∴![]() ,
,
![]()
∴![]() .
.
設直線![]() 的表達式為
的表達式為![]()
將![]() 和
和![]() 代入,得
代入,得
![]() ,
,
解得![]() ,
,
∴直線![]() 的函數表達式
的函數表達式![]() .
.
(3)如圖3,分兩種情況,點Q可在x軸下方和點Q在x軸上方
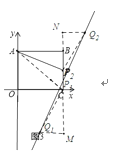
設點Q坐標為![]() ,點P坐標為
,點P坐標為![]()
當點Q在x軸下方時,連接![]() ,過點
,過點![]() 作
作![]() 交其延長線于M,則M點坐標為
交其延長線于M,則M點坐標為![]()
![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
由題意得![]()
![]() ,
,![]()
解得![]() ,所以
,所以![]()
當點Q在x軸上方時,連接![]() ,過點
,過點![]() 作
作![]() 交其延長線于N,則N點坐標為
交其延長線于N,則N點坐標為![]()
同理可得![]() ,
,![]()
由題意得![]()
![]() ,
,![]()
解得![]() ,所以
,所以
綜上![]() 的坐標為:
的坐標為:![]() .
.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:初中數學 來源: 題型:
【題目】閱讀下列材料,完成任務:
自相似圖形
定義:若某個圖形可分割為若干個都與它相似的圖形,則稱這個圖形是自相似圖形.例如:正方形ABCD中,點E、F、G、H分別是AB、BC、CD、DA邊的中點,連接EG,HF交于點O,易知分割成的四個四邊形AEOH、EBFO、OFCG、HOGD均為正方形,且與原正方形相似,故正方形是自相似圖形.
任務:
(1)圖1中正方形ABCD分割成的四個小正方形中,每個正方形與原正方形的相似比為 ;
(2)如圖2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明發現△ABC也是“自相似圖形”,他的思路是:過點C作CD⊥AB于點D,則CD將△ABC分割成2個與它自己相似的小直角三角形.已知△ACD∽△ABC,則△ACD與△ABC的相似比為 ;
(3)現有一個矩形ABCD是自相似圖形,其中長AD=a,寬AB=b(a>b).
請從下列A、B兩題中任選一條作答:我選擇 題.
A:①如圖3﹣1,若將矩形ABCD縱向分割成兩個全等矩形,且與原矩形都相似,則a= (用含b的式子表示);
②如圖3﹣2若將矩形ABCD縱向分割成n個全等矩形,且與原矩形都相似,則a= (用含n,b的式子表示);
B:①如圖4﹣1,若將矩形ABCD先縱向分割出2個全等矩形,再將剩余的部分橫向分割成3個全等矩形,且分割得到的矩形與原矩形都相似,則a= (用含b的式子表示);
②如圖4﹣2,若將矩形ABCD先縱向分割出m個全等矩形,再將剩余的部分橫向分割成n個全等矩形,且分割得到的矩形與原矩形都相似,則a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的△ABC,若小方格邊長為1,格點△ABC(頂點是網格線交點的三角形)的頂點A,C的坐標分別為(﹣1,1),(0,﹣2),請你根據所學的知識.
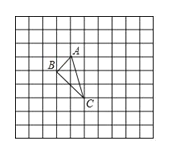
(1)在如圖所示的網格平面內作出平面直角坐標系;
(2)作出△ABC關于y軸對稱的三角形A1B1C1;
(3)判斷△ABC的形狀,并求出△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為培養學生的特長愛好,提高學生的綜合素質,某校音樂特色學習斑準備從京東商城里一次性購買若干個尤克里里和豎笛(每個尤克里里的價格相同,每個豎笛的價格相同),購買![]() 個豎笛和
個豎笛和![]() 個尤克里里共需
個尤克里里共需![]() 元;豎笛單價比尤克里里單價的一半少
元;豎笛單價比尤克里里單價的一半少![]() 元.
元.
(1)求豎笛和尤克里里的單價各是多少元?
(2)根據學校實際情況,需一次性購買豎笛和尤克里里共![]() 個,但要求購買豎笛和尤克里里的總費用不超過
個,但要求購買豎笛和尤克里里的總費用不超過![]() 元,則該校最多可以購買多少個尤克里里?
元,則該校最多可以購買多少個尤克里里?
查看答案和解析>>
科目:初中數學 來源: 題型:
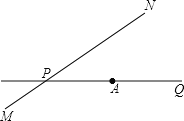
【題目】如圖,公路MN和公路PQ在點P處交匯,且∠QPN=30°,點A處有一所中學,AP=160m.若拖拉機行駛時,周圍100m以內會受到噪音的影響,那么拖拉機在公路MN上沿PN方向行駛時:
(1)學校是否會受到噪聲影響?
(2)如果不受影響,請說明理由;如果受影響,已知拖拉機的速度為18km/h,那么學校受影響的時間為多少秒?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【操作發現】
如圖①,在邊長為1個單位長度的小正方形組成的網格中,△ABC的三個頂點均在格點上.

(1)請按要求畫圖:將△ABC繞點A按順時針方向旋轉90°,點B的對應點為B′,點C的對應點為C′,連接BB′;
(2)在(1)所畫圖形中,∠AB′B= .
【問題解決】
如圖②,在等邊三角形ABC中,AC=7,點P在△ABC內,且∠APC=90°,∠BPC=120°,求△APC的面積.
小明同學通過觀察、分析、思考,對上述問題形成了如下想法:
想法一:將△APC繞點A按順時針方向旋轉60°,得到△AP′B,連接PP′,尋找PA,PB,PC三條線段之間的數量關系;
想法二:將△APB繞點A按逆時針方向旋轉60°,得到△AP′C′,連接PP′,尋找PA,PB,PC三條線段之間的數量關系.
…
請參考小明同學的想法,完成該問題的解答過程.(一種方法即可)
【靈活運用】
如圖③,在四邊形ABCD中,AE⊥BC,垂足為E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k為常數),求BD的長(用含k的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
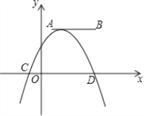
【題目】如圖,點A,B的坐標分別為(1,4)和(4,4),拋物線y=a(x+m)2+n的頂點在線段AB上,與x軸交于C,D兩點(C在D的左側),點C的橫坐標最小值為﹣3,則點D的橫坐標的最大值為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com