
【題目】已知銳角∠AOB,如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;(2)分別以點C,D為圓心,CD長為半徑作弧,兩弧交于點P,連接CP,DP;(3)作射線OP交CD于點Q.根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
,交射線OB于點D,連接CD;(2)分別以點C,D為圓心,CD長為半徑作弧,兩弧交于點P,連接CP,DP;(3)作射線OP交CD于點Q.根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
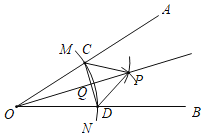
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
【答案】A
【解析】
由作圖知OC=OD,CD=CP=DP,根據等邊三角形的判定和性質、線段垂直平分線的性質和判定、角平分線的基本作圖,逐一判斷可得.
由作圖可知:射線OP即為∠AOB的角平分線,
∴∠AOP=∠BOP,
故C正確,不符合題意;
由作圖(1)(2)可知:OC=OD,CP=DP,
∴OP是CD的垂直平分線,
∴CD⊥OP,
故D正確,不符合題意;
由作圖(2)可知:CD=CP=PD,
∴△CDP是等邊三角形,
∵CD⊥OP,
∴CP=2CQ,
故B正確,不符合題意;
∵∠AOP=∠BOP,
當OC=CP時,∠AOP=∠CPO,
∴∠CPO=∠BOP,
∴CP∥OB,
故A錯誤,符合題意;
故選:A.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:初中數學 來源: 題型:
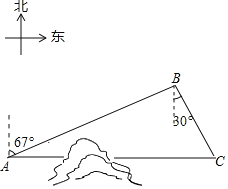
【題目】如圖,C地在A地的正東方向,因有大山阻隔,由A地到C地需要繞行B地,已知B地位于A地北偏東67°方向,距離A地520km,C地位于B地南偏東30°方向,若打通穿山隧道,建成兩地直達高鐵,求A地到C地之間高鐵線路的長(結果保留整數)(參考數據:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,扇形OAB中,∠AOB=90°,將扇形OAB繞點B逆時針旋轉,得到扇形BDC,若點O剛好落在弧AB上的點D處,則![]() 的值為( )
的值為( )
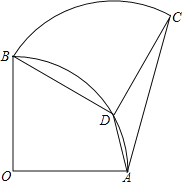
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】全球已經進入大數據時代,大數據(![]() )是指數據規模巨大,類型多樣且信息傳播速度快的數據庫體系.大數據在推動經濟發展,改善公共服務等方面日益顯示出巨大的價值為創建大數據應用示范城市,我市某機構針對市民最關心的四類生活信息進行了民意調查(被調查者每人限送一項),下面是根據調查結果繪制出不完整的兩個統計圖表:
)是指數據規模巨大,類型多樣且信息傳播速度快的數據庫體系.大數據在推動經濟發展,改善公共服務等方面日益顯示出巨大的價值為創建大數據應用示范城市,我市某機構針對市民最關心的四類生活信息進行了民意調查(被調查者每人限送一項),下面是根據調查結果繪制出不完整的兩個統計圖表:
生活信息關注度條形統計圖
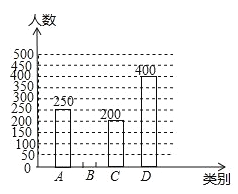
A:政府服務信息 B:城市醫療信息 C:交于資源信息 D:交通信息
生活信息關注度扇形統計圖
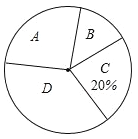
請根據圖中提供的信息,解答下列問題:
(1)本次參與調查的人數是______,扇形統計圖中![]() 部分的圓心角的度數是_______.并補全條形統計圖;
部分的圓心角的度數是_______.并補全條形統計圖;
(2)這次調查的市民最關心的四類生活信息的眾數是_______類;
(3)若我市現有常住人口約600萬,請你估計最關心“城市醫療信息”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
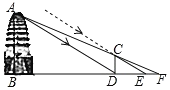
【題目】如圖,西安市薦福寺內的小雁塔,是中國早期方形密檐式磚塔的典型作品,并作為絲綢之路的一處重要遺址點,被列入《世界遺產名錄》.某周末,小樂和小夏相約去小雁塔游玩,在休息時,他們想利用所學知識測量小雁塔的高度,于是他們向工作人員借來測量工具由于觀測點與小雁塔底部間的距離不易測量,于是他們利用太陽光照射影子進行測量,小樂先在小雁塔的影子頂端![]() 處豎直立一根長1.72米的木棒
處豎直立一根長1.72米的木棒![]() ,并測得此時木棒的影長
,并測得此時木棒的影長![]() 米;然后小夏在
米;然后小夏在![]() 的延長線上找出一點
的延長線上找出一點![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三點在同一直線上,并測得
三點在同一直線上,并測得![]() 米已知圖中所有點均在同一平面內,
米已知圖中所有點均在同一平面內,![]() ,
,![]() ,根據以上測量過程及數據,請你幫他們求出小雁塔的高度
,根據以上測量過程及數據,請你幫他們求出小雁塔的高度![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,BE⊥CD于點E,DF⊥BC于點F.
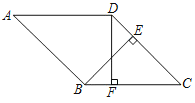
(1)求證:BF=DE;
(2)分別延長BE和AD,交于點G,若∠A=45°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,CD是△ABC的中線,如果![]() 上的所有點都在△ABC的內部或邊上,則稱
上的所有點都在△ABC的內部或邊上,則稱![]() 為△ABC的中線弧.
為△ABC的中線弧.
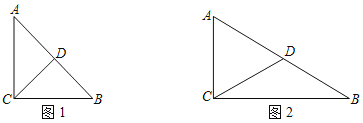
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中點.
①如圖1,若∠A=45°,畫出△ABC的一條中線弧![]() ,直接寫出△ABC的中線弧
,直接寫出△ABC的中線弧![]() 所在圓的半徑r的最小值;
所在圓的半徑r的最小值;
②如圖2,若∠A=60°,求出△ABC的最長的中線弧![]() 的弧長l.
的弧長l.
(2)在平面直角坐標系中,已知點A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中點.求△ABC的中線弧![]() 所在圓的圓心P的縱坐標t的取值范圍.
所在圓的圓心P的縱坐標t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小菲設計的“作一個角等于已知角的二倍”的尺規作圖過程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如圖,
①分別以點![]() 和點
和點![]() 為圓心,大于
為圓心,大于![]() 的長為半徑作弧,兩弧交于
的長為半徑作弧,兩弧交于![]() 、
、![]() 點,作直線
點,作直線![]() ;
;
②分別以點![]() 和點
和點![]() 為圓心,大于
為圓心,大于![]() 的長為半徑作弧,兩弧交于
的長為半徑作弧,兩弧交于![]() 、
、![]() 點,作直線
點,作直線![]() ,
,![]() 和
和![]() 交于點
交于點![]() ;
;
③連接![]() 和
和![]() ;
;
④以點![]() 為圓心,
為圓心,![]() 的長為半徑作
的長為半徑作![]() .
.
所以![]() .
.
根據小菲設計的尺規作圖過程.
(1)使用直尺和圓規,補全圖形(保留作圖痕跡);

(2)完成下面的證明.

證明:連接![]()
∵![]() 和
和![]() 分別為
分別為![]() 、
、![]() 的垂直平分線,
的垂直平分線,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圓.
的外接圓.
∵點![]() 是
是![]() 上的一點,
上的一點,
∴![]() .(____________).(填推理的依據)
.(____________).(填推理的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
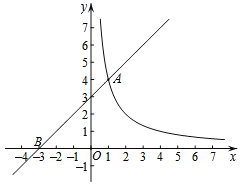
【題目】如圖,在平面直角坐標系xOy中,直線y=x+3與函數y=![]() (x>0)的圖象交于點A(1,m),與x軸交于點B.
(x>0)的圖象交于點A(1,m),與x軸交于點B.
(1)求m,k的值;
(2)過動點P(0,n)(n>0)作平行于x軸的直線,交函數y=![]() (x>0)的圖象于點C,交直線y=x+3于點D.
(x>0)的圖象于點C,交直線y=x+3于點D.
①當n=2時,求線段CD的長;
②若CD≥OB,結合函數的圖象,直接寫出n的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com