題目列表(包括答案和解析)
閱讀理解：對于任意正實數a、b，∵(
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有當a＝b時，等號成立.
結論：在a＋b≥2（a、b均為正實數）中，若ab為定值p，則a+b≥2
，只有當a＝b時，a＋b有最小值2. 根據上述內容，回答下列問題：
（1）若m＞0，只有當m＝ 時，m＋
有最小值 ；
若m＞0，只有當m＝ 時，2m＋
有最小值 .
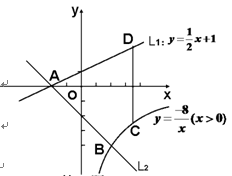
（2）如圖，已知直線L1：y＝
x＋1與x軸交于點A，過點A的另一直線L2與雙曲線y＝
（x>0）相交于點B（2，m），求直線L2的解析式.
（3）在（2）的條件下，若點C為雙曲線上任意一點，作CD∥y軸交直線L1于點D，試
求當線段CD最短時，點A、B、C、D圍成的四邊形面積.
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有當a＝b時，等號成立.（a、b均為正實數）中，若ab為定值p，則a+b≥2
，只有當a＝b時，a＋b有最小值2. 根據上述內容，回答下列問題：
有最小值 ；
有最小值 .
x＋1與x軸交于點A，過點A的另一直線L2與雙曲線y＝
閱讀理解：對于任意正實數a、b，∵(
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有當a＝b時，等號成立.
結論：在a＋b≥2（a、b均為正實數）中，若ab為定值p，則a+b≥2
，只有當a＝b時，a＋b有最小值2. 根據上述內容，回答下列問題：
（1）若m＞0，只有當m＝ 時，m＋
有最小值 ；
若m＞0，只有當m＝ 時，2m＋
有最小值 .
（2）如圖，已知直線L1：y＝
x＋1與x軸交于點A，過點A的另一直線L2與雙曲線y＝
（x>0）相交于點B（2，m），求直線L2的解析式.
（3）在（2）的條件下，若點C為雙曲線上任意一點，作CD∥y軸交直線L1于點D，試
求當線段CD最短時，點A、B、C、D圍成的四邊形面積.
閱讀理解：對于任意正實數a、b，∵(
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有當a＝b時，等號成立.
結論：在a＋b≥2（a、b均為正實數）中，若ab為定值p，則a+b≥2
，只有當a＝b時，a＋b有最小值2.
根據上述內容，回答下列問題：
（1）若m＞0，只有當m＝ 時，m＋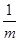
有最小值 ；
若m＞0，只有當m＝ 時，2m＋
有最小值 .
（2）如圖，已知直線L1：y＝
x＋1與x軸交于點A，過點A的另一直線L2與雙曲線y＝
（x>0）相交于點B（2，m），求直線L2的解析式.
（3）在（2）的條件下，若點C為雙曲線上任意一點，作CD∥y軸交直線L1于點D，試
求當線段CD最短時，點A、B、C、D圍成的四邊形面積.
－
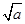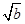)2≥0，∴a－2
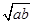＋b≥0，∴a＋b≥2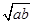，只有當a＝b時，等號成立.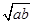（a、b均為正實數）中，若ab為定值p，則a+b≥2
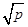，只有當a＝b時，a＋b有最小值2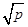. 根據上述內容，回答下列問題：
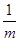有最小值 ；
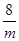有最小值 .
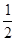x＋1與x軸交于點A，過點A的另一直線L2與雙曲線y＝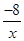
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com