
題目列表(包括答案和解析)
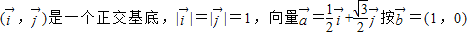 平移所掃過平面部分的面積等于( )
平移所掃過平面部分的面積等于( )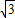
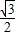

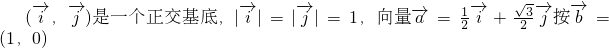 平移所掃過平面部分的面積等于
平移所掃過平面部分的面積等于


| i |
| j |
| i |
| j |
| a |
| 1 |
| 2 |
| i |
| ||
| 2 |
| j |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
| i |
| j |
| i |
| j |
| a |
| 1 |
| 2 |
| i |
| ||
| 2 |
| j |
| b |
A.
| B.
| C.
| D.1 |
一、選擇題:本小題共8小題,每小題5分,共40分.
題號
1
2
3
4
5
6
7
8
答案
B
D
B
B
A
C
B
C
二、填空題:本小題9―12題必答,13、14、15小題中選答2題,若全答只計(jì)前兩題得分,共30分.
9. 35
10. 08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image120.gif) 11.
11.
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image122.gif) 12.
12. 08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image124.gif)
13.
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image126.gif) 或
或08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image128.gif) 14. 10
15.
14. 10
15. 08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image130.gif)
三、解答題:共80分.
16題(本題滿分13分)
解:(1)要使f(x)有意義,必須08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image132.gif) ,即
,即08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image134.gif)
得f(x)的定義域?yàn)?sub>08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image136.gif) ………………………………4分
………………………………4分
(2)因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image138.gif) 在
在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image140.gif) 上,
上,
當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image142.gif) 時(shí)取得最大值
時(shí)取得最大值08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image144.gif) ………………………………………5分
………………………………………5分
當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image146.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image140.gif) 時(shí),
時(shí),08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image148.gif) ,得f(x)的遞減區(qū)間為
,得f(x)的遞減區(qū)間為
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image150.gif) ,遞增區(qū)間為
,遞增區(qū)間為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image152.gif) ……9分
……9分
(3)因f(x)的定義域?yàn)?sub>08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image136.gif) ,關(guān)于原點(diǎn)不對稱,所以f(x)為非奇非偶函數(shù). ……………………………………………………………………13分
,關(guān)于原點(diǎn)不對稱,所以f(x)為非奇非偶函數(shù). ……………………………………………………………………13分
17題(本題滿分13分)
解:(1)當(dāng)且僅當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image154.gif) 時(shí),方程組有唯一解.因
時(shí),方程組有唯一解.因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image156.gif) 的可能情況為
的可能情況為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image158.gif) 三種情況………………………………3分
三種情況………………………………3分
而先后兩次投擲骰子的總事件數(shù)是36種,所以方程組有唯一解的概率
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image160.gif) ……………………………………………………………………6分
……………………………………………………………………6分
(2)因?yàn)榉匠探M只有正數(shù)解,所以兩直線的交點(diǎn)在第一象限,由它們的圖像可知
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image162.gif) ………………………………………………………………9分
………………………………………………………………9分
解得(a,b)可以是(1,4),(1,5),(1,6),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2),(5,1),(5,2),(6,1),(6,2),所以方程組只有正數(shù)解的概率08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image164.gif) ………………………………………………………………………13分
………………………………………………………………………13分
18題(本題滿分14分)
解:(1)因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image166.gif) ,所以AD⊥平面CDE,ED是AE在平面CDE上的射影,∠AED=450,所以直線AE與平面CDE所成的角為450………………………………4分(2)解法一:如圖,取AB、AD所在直線為x軸、y軸建立直角坐標(biāo)系A(chǔ)―xyz.
,所以AD⊥平面CDE,ED是AE在平面CDE上的射影,∠AED=450,所以直線AE與平面CDE所成的角為450………………………………4分(2)解法一:如圖,取AB、AD所在直線為x軸、y軸建立直角坐標(biāo)系A(chǔ)―xyz.
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image167.gif) 則
則08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image169.gif) ………5分
………5分
設(shè)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image171.gif) ,
,
得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image173.gif) …………9分
…………9分
由08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image175.gif) ,得
,得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image177.gif) ,而
,而08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image179.gif) 是平面CDE的一個(gè)法向量,且
是平面CDE的一個(gè)法向量,且08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image181.gif) 平面CDE,
平面CDE,
所以MN//平面CDE…………………………………………………………………………14分
解法二:設(shè)在翻轉(zhuǎn)過程中,點(diǎn)M到平面CDE的距離為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image183.gif) ,點(diǎn)N到平面CDE的距離為
,點(diǎn)N到平面CDE的距離為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image185.gif) ,則
,則08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image187.gif) ,同理
,同理08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image189.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image190.gif) 所以
所以08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image192.gif) ,故MN//平面CDE……………………………………………………………14分
,故MN//平面CDE……………………………………………………………14分
解法三:如圖,過M作MQ//AD交ED于點(diǎn)Q,
過N作NP//AD交CD于點(diǎn)P,
連接MN和PQ…………………………………5分
設(shè)ㄓADE向上翻折的時(shí)間為t,則08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image194.gif) ,
,08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image196.gif) ………………7分
………………7分
因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image198.gif) ,點(diǎn)D是CE的中點(diǎn),得
,點(diǎn)D是CE的中點(diǎn),得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image200.gif) ,四邊形ABCD為正方形,ㄓADE為等腰三角形.
,四邊形ABCD為正方形,ㄓADE為等腰三角形. 08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image202.gif) ……………………10分
……………………10分
在RtㄓEMQ和RtㄓDNP中,ME=ND,∠MEQ=∠NDP=450,所以RtㄓEMQ≌RtㄓDNP,
所以MQ//NP且MQ=NP,的四邊形MNPQ為平行四邊形,所以MN//PQ,因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image181.gif) 平面CDE,
平面CDE,
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image205.gif) 平面CDE,所以MN//平面CDE……………………………………………………14分
平面CDE,所以MN//平面CDE……………………………………………………14分
19題(本題滿分14分)
解:(1)由已知得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image207.gif) ,解得:
,解得:08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image209.gif) ……………………2分
……………………2分
所求橢圓方程為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image211.gif) ………………………………………………4分
………………………………………………4分
(2)因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image213.gif) ,得
,得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image215.gif) ……………………………………7分
……………………………………7分
(3)因點(diǎn)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image217.gif) 即A(3,0),設(shè)直線PQ方程為
即A(3,0),設(shè)直線PQ方程為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image219.gif) ………………8分
………………8分
則由方程組08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image221.gif) ,消去y得:
,消去y得:08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image223.gif)
設(shè)點(diǎn)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image225.gif) 則
則08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image227.gif) ……………………10分
……………………10分
因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image229.gif) ,得
,得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image231.gif) ,
,
又08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image233.gif) ,代入上式得
,代入上式得
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image235.gif) ,故
,故08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image237.gif)
解得:08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image239.gif) ,所求直線PQ方程為
,所求直線PQ方程為08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image241.gif) ……………………14分
……………………14分
20題(本題滿分14分)
解:(1)函數(shù)f(x)的定義域?yàn)?sub>08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image243.gif) ,
,08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image245.gif) …………2分
…………2分
①當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image247.gif) 時(shí),
時(shí),08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image249.gif) >0,f(x)在
>0,f(x)在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image243.gif) 上遞增.………………………………4分
上遞增.………………………………4分
②當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image251.gif) 時(shí),令
時(shí),令08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image253.gif) 得
得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image255.gif) 解得:
解得:
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image257.gif) ,因
,因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image259.gif) (舍去),故在
(舍去),故在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image261.gif) 上
上08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image249.gif) <0,f(x)遞減;在
<0,f(x)遞減;在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image263.gif) 上,
上,08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image249.gif) >0,f(x)遞增.…………8分
>0,f(x)遞增.…………8分
(2)由(1)知08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image265.gif) 在
在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image267.gif) 內(nèi)遞減,在
內(nèi)遞減,在08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image269.gif) 內(nèi)遞增.
內(nèi)遞增.
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image271.gif) ……………………………………11分
……………………………………11分
故08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image273.gif) ,又因
,又因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image275.gif)
故08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image277.gif) ,得
,得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image279.gif) ………………14分
………………14分
21題(本題滿分12分)
解:(1)
解法一:由08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image281.gif) ,可得
,可得
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image283.gif) ………………………………2分
………………………………2分
所以08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image285.gif) 是首項(xiàng)為0,公差為1的等差數(shù)列.
是首項(xiàng)為0,公差為1的等差數(shù)列.
所以08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image287.gif) 即
即08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image289.gif) ……………………4分
……………………4分
解法二:因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image291.gif) 且
且08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image293.gif) 得
得
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image295.gif) ,
,
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image297.gif) ,
,
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image299.gif) ,
,
…………………………………………………………
由此可猜想數(shù)列08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image301.gif) 的通項(xiàng)公式為:
的通項(xiàng)公式為:08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image289.gif) …………2分
…………2分
以下用數(shù)學(xué)歸納法證明:
①當(dāng)n=1時(shí),08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image291.gif) ,等式成立;
,等式成立;
②假設(shè)當(dāng)n=k時(shí),有08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image303.gif) 成立,那么當(dāng)n=k+1時(shí),
成立,那么當(dāng)n=k+1時(shí),
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image305.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image307.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image309.gif) 成立
成立
所以,對于任意08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image311.gif) ,都有
,都有08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image313.gif) 成立……………………4分
成立……………………4分
(2)解:設(shè)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image315.gif) ……①
……①
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image317.gif) ……②
……②
當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image319.gif) 時(shí),①
時(shí),①08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image321.gif) ②得
②得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image323.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image325.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image327.gif) …………6分
…………6分
這時(shí)數(shù)列08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image301.gif) 的前n項(xiàng)和
的前n項(xiàng)和08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image329.gif)
當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image331.gif) 時(shí),
時(shí),08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image333.gif) ,這時(shí)數(shù)列
,這時(shí)數(shù)列08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image301.gif) 的前n項(xiàng)和
的前n項(xiàng)和
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image335.gif) …………………………………………8分
…………………………………………8分
(3)證明:因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image337.gif) 得
得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image339.gif) ,顯然存在k=1,使得對任意
,顯然存在k=1,使得對任意08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image311.gif) ,
,
有08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image342.gif) 成立;…………………………………………9分
成立;…………………………………………9分
①當(dāng)n=1時(shí),等號成立;
②當(dāng)08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image344.gif) 時(shí),因
時(shí),因08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image346.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image348.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image350.gif)
08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image352.gif)
所以,存在k=1,使得08-09學(xué)年度第一學(xué)期期末高三級質(zhì)檢理科數(shù)學(xué)試題.files/image354.gif) 成立……………12分
成立……………12分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com