
題目列表(包括答案和解析)
| 3 |
| 3 |
.如圖是函數![]() 的圖象,則其解析式是( )
的圖象,則其解析式是( )
A.![]()
B.![]()
C.![]()
D. ![]()
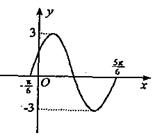
C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B錯;
,故B錯;![]() +
+![]() =
=![]() =
=![]() ≥4,故A錯;由基本不等式得
≥4,故A錯;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正確;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正確;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D錯.故選C.
,故D錯.故選C.
.本小題滿分15分)
如圖,已知橢圓E: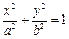
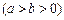 ,焦點為
,焦點為 、
、 ,雙曲線G:
,雙曲線G: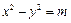
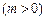 的頂點是該橢
的頂點是該橢 圓的焦點,設
圓的焦點,設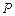 是雙曲線G上異于頂點的任一點,直線
是雙曲線G上異于頂點的任一點,直線 、
、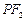 與橢圓的交點分別為A、B和C、D,已知三角形
與橢圓的交點分別為A、B和C、D,已知三角形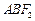 的周長等于
的周長等于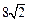 ,橢圓四個頂點組成的菱形的面積為
,橢圓四個頂點組成的菱形的面積為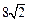 .
.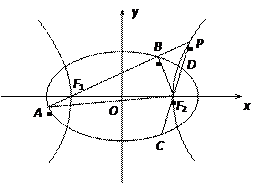
(1)求橢圓E與雙曲線G的方程;
(2)設直線 、
、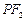 的斜率分別為
的斜率分別為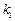 和
和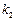 ,探求
,探求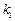 和
和
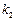 的關系;
的關系;
(3)是否存在常數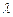 ,使得
,使得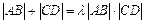 恒成立?
恒成立?
若存在,試求出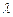 的值;若不存在, 請說明理由.
的值;若不存在, 請說明理由.
.定義域為R的函數 滿足
滿足 ,且當
,且當 時,
時, ,則當
,則當 時,
時, 的最小值為( )
的最小值為( )
(A) (B)
(B) (C)
(C) (D)
(D)
一、選擇題:本大題主要考查基本知識和基本運算.共10小題,每小題5分,滿分50分.
題號
1
2
3
4
5
6
7
8
9
10
答案
C
A
B
A
B
C
D
C
B
D
二、填空題:本大題主要考查基本知識和基本運算.本大題共5小題,考生作答4小題,每小題5分,滿分20分.其中14~15題是選做題,考生只能選做一題.
11. 12.
12. 13.
13. 14.
14. 15.2
15.2
說明:第14題答案可以有多種形式,如可答 或
或 Z)等, 均給滿分.
Z)等, 均給滿分.
三、解答題:本大題共6小題,滿分80分.解答須寫出文字說明、證明過程和演算步驟.
16.(本小題滿分12分)
解:(1)∵


 .
6分
.
6分
∴ .
8分
.
8分
(2) 當 時,
時,  取得最大值, 其值為2 . ……………………10分
取得最大值, 其值為2 . ……………………10分
此時 ,即
,即
 Z
Z . ……………………12分
. ……………………12分
17. (本小題滿分12分)
解:(1) 由頻率分布條形圖知,抽取的學生總數為 人. ………… 3分
人. ………… 3分
∵各班被抽取的學生人數成等差數列,設其公差為 ,
,
由 =100,解得
=100,解得 . …………………………………… 6分
. …………………………………… 6分
∴各班被抽取的學生人數分別是22人,24人,26人,28人. …… 8分
(2) 在抽取的學生中,任取一名學生, 則分數不小于90分的概率為0.35+0.25+0.1+0.05=0.75. ………………………………12分
18.(本小題滿分14分)
解:(1)∵  ⊥平面
⊥平面 ,
,
 平面
平面 ,
,
∴
 ⊥
⊥ .
………………………………………………2分
.
………………………………………………2分
∵
 ⊥
⊥ ,
,


 ,
,
∴
 ⊥平面
⊥平面 , ……………………………………………………4分
, ……………………………………………………4分
∵

 平面
平面 ,
,
∴
 ⊥
⊥ . …………………………………………………………6分
. …………………………………………………………6分
 (2)法1: 取線段
(2)法1: 取線段 的中點
的中點 ,
, 的中點
的中點 ,連結
,連結 ,
,
則 是△
是△ 中位線.
中位線.
∴ ∥
∥ ,
, , …………………………8分
, …………………………8分
∵
 ,
, ,
,
∴ .
.
∴
四邊形 是平行四邊形, …………………………10分
是平行四邊形, …………………………10分
∴  .
.
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 . …………………………………… 13分
. …………………………………… 13分
∴
線段 的中點
的中點 是符合題意要求的點. ……………………………………14分
是符合題意要求的點. ……………………………………14分
法2: 取線段 的中點
的中點 ,
, 的中點
的中點 ,連結
,連結 ,
,
 則
則 是△
是△ 的中位線.
的中位線.
∴ ∥
∥ ,
, , …………………………8分
, …………………………8分
∵ 平面
平面 ,
,  平面
平面 ,
,
∴ 平面
平面 .
.
∵
 ,
, ,
,
∴ .
.
∴
四邊形 是平行四邊形, ……………………………………10分
是平行四邊形, ……………………………………10分
∴  .
.
∵ 
 平面
平面 ,
,
 平面
平面 ,
,
∴  ∥平面
∥平面 .
.
∵ ,
,
∴平面 平面
平面 .……………………………………………………12分
.……………………………………………………12分
∵ 平面
平面 ,
,
∴ ∥平面
∥平面 .
.
∴
線段 的中點
的中點 是符合題意要求的點.……………………………… 14分
是符合題意要求的點.……………………………… 14分
19. (本小題滿分14分)
解:(1)依題意知, …………………………………………2分
…………………………………………2分
∵ ,
,
∴ . ………………………………………… 5分
. ………………………………………… 5分
∴所求橢圓 的方程為
的方程為 . …………………………………………6分
. …………………………………………6分
(2)∵ 點
 關于直線
關于直線 的對稱點為
的對稱點為 ,
,
∴ 
解得: ,
, .
…………………………8分
.
…………………………8分
∴ .
……………………………10分
.
……………………………10分
∵
點
 在橢圓
在橢圓 :
: 上,
上,
∴ , 則
, 則 .………………………………………………12分
.………………………………………………12分
∴ 的取值范圍為
的取值范圍為 . …………………………………………14分
. …………………………………………14分
20. (本小題滿分14分)
(1) 解:當 時,
時, .
……………………………………1分
.
……………………………………1分
當 時,
時,

 .
…………………………………………4分
.
…………………………………………4分
∵ 不適合上式,
不適合上式,
∴ ………………………………………………………5分
………………………………………………………5分
(2)證明: ∵ .
.
當 時,
時, ………………………………………………6分
………………………………………………6分
當 時,
時, ,
①
,
①
 . ②
. ②
①-②得:


得 , …………………………………………10分
, …………………………………………10分
此式當 時也適合.
時也適合.
∴ N
N .
.
∵ ,
,
∴ .
…………………………………………………11分
.
…………………………………………………11分
當 時,
時, ,
,
∴ .
.
∵ ,
,
∴ .
.
故 ,即
,即 . ……………………………………………13分
. ……………………………………………13分
綜上, .
………………………………14分
.
………………………………14分
21. (本小題滿分14分)
解:(1)當 時,
時, ,
,
∴
 .
.
令 =0, 得
=0, 得  .
………………………………………………2分
.
………………………………………………2分
當 時,
時, , 則
, 則 在
在 上單調遞增;
上單調遞增;
當 時,
時, , 則
, 則 在
在 上單調遞減;
上單調遞減;
當 時,
時, ,
,  在
在 上單調遞增.
…………………………2分
上單調遞增.
…………………………2分
∴ 當 時,
時,  取得極大值為
取得極大值為
 ;…………………………4分
;…………………………4分
當 時,
時,  取得極小值為
取得極小值為
 . ………………………6分
. ………………………6分
(2) ∵  =
=  ,
,
∴△=  =
=  .
.
① 若a≥1,則△≤0,
∴ ≥0在R上恒成立,
≥0在R上恒成立,
∴ f(x)在R上單調遞增 .
∵f(0) ,
, ,
,
∴當a≥1時,函數f(x)的圖象與x軸有且只有一個交點. ……………………9分
② 若a<1,則△>0,
∴ = 0有兩個不相等的實數根,不妨設為x1,x2,(x1<x2).
= 0有兩個不相等的實數根,不妨設為x1,x2,(x1<x2).
∴x1+x2 = 2,x1x2 = a.
當 變化時,
變化時, 的取值情況如下表:
的取值情況如下表:
x

x1
(x1,x2)
x2


+
0
-
0
+
f(x)
ㄊ
極大值
ㄋ
極小值
ㄊ
∵ ,
,
∴ .
.
∴



 .
.
同理
 .
.
∴


 .
.
令f(x1)?f(x2)>0, 解得a> .
.
而當 時,
時, ,
,
故當 時, 函數f(x)的圖象與x軸有且只有一個交點.
時, 函數f(x)的圖象與x軸有且只有一個交點.
綜上所述,a的取值范圍是 .
……………………………………14分
.
……………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com