(3)若對于任意的上恒成立.求的取值范圍. 【查看更多】

對于定義在D上的函數y=f（x），若同時滿足①存在閉區間[a，b]⊆D，使得任取x₁∈[a，b]，都有f（x₁）=c（c是常數）；②對于D內任意x₂，當x₂∉[a，b]時總有f（x₂）＞c；則稱f（x）為“平底型”函數．
（1）判斷f₁（x）=|x-1|+|x-2|，f₂（x）=x+|x-2|是否是“平底型”函數？簡要說明理由；
（2）設f（x）是（1）中的“平底型”函數，若|t-k|+|t+k|≥|k|•f（x），（k∈R，k≠0）對一切t∈R恒成立，求實數x的范圍；
（3）若F(x)=mx+

x2+2x+n

，x∈[-2，+∞)是“平底型”函數，求m和n的值．

查看答案和解析>>

對于定義在D上的函數y=f（x），若同時滿足①存在閉區間[a，b]⊆D，使得任取x₁∈[a，b]，都有f（x₁）=c（c是常數）；②對于D內任意x₂，當x₂∉[a，b]時總有f（x₂）＞c；則稱f（x）為“平底型”函數．
（1）判斷f₁（x）=|x-1|+|x-2|，f₂（x）=x+|x-2|是否是“平底型”函數？簡要說明理由；
（2）設f（x）是（1）中的“平底型”函數，若|t-k|+|t+k|≥|k|•f（x），（k∈R，k≠0）對一切t∈R恒成立，求實數x的范圍；
（3）若

是“平底型”函數，求m和n的值．

查看答案和解析>>

對于定義在D上的函數y=f（x），若同時滿足①存在閉區間[a，b]⊆D，使得任取x₁∈[a，b]，都有f（x₁）=c（c是常數）；②對于D內任意x₂，當x₂∉[a，b]時總有f（x₂）＞c；則稱f（x）為“平底型”函數．
（1）判斷f₁（x）=|x-1|+|x-2|，f₂（x）=x+|x-2|是否是“平底型”函數？簡要說明理由；
（2）設f（x）是（1）中的“平底型”函數，若|t-k|+|t+k|≥|k|•f（x），（k∈R，k≠0）對一切t∈R恒成立，求實數x的范圍；
（3）若

是“平底型”函數，求m和n的值．

查看答案和解析>>

對于定義在D上的函數y=f（x），若同時滿足①存在閉區間[a，b]⊆D，使得任取x₁∈[a，b]，都有f（x₁）=c（c是常數）；②對于D內任意x₂，當x₂∉[a，b]時總有f（x₂）＞c；則稱f（x）為“平底型”函數．
（1）判斷f₁（x）=|x-1|+|x-2|，f₂（x）=x+|x-2|是否是“平底型”函數？簡要說明理由；
（2）設f（x）是（1）中的“平底型”函數，若|t-k|+|t+k|≥|k|•f（x），（k∈R，k≠0）對一切t∈R恒成立，求實數x的范圍；
（3）若 $數學公式$ 是“平底型”函數，求m和n的值．

查看答案和解析>>

對于函數f₁（x），f₂（x），h（x），如果存在實數a，b使得h（x）=a•f₁（x）+b•f₂（x），那么稱h（x）為f₁（x），f₂（x）的生成函數．
（1）下面給出兩組函數，h（x）是否分別為f₁（x），f₂（x）的生成函數？并說明理由．
第一組： $數學公式$ ；
第二組：f₁（x）=x²-x，f₂（x）=x²+x+1，h（x）=x²-x+1．
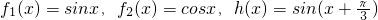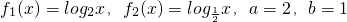（2）設 $數學公式$ ，生成函數h（x）．若不等式h（4x）+t•h（2x）＜0在x∈[2，4]上有解，求實數t的取值范圍．
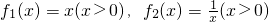（3）設 $數學公式$ ，取a＞0，b＞0生成函數h（x）圖象的最低點坐標為（2，8）．若對于任意正實數x₁，x₂且x₁+x₂=1，試問是否存在最大的常數m，使h（x₁）h（x₂）≥m恒成立？如果存在，求出這個m的值；如果不存在，請說明理由．

查看答案和解析>>

一、選擇題：本大題共12小題，每小題5分，共60分。

BADD CCCB AADB

二、填空題：本大題共4小題，每小題4分，共16分。

13．

14．

15．-2

16．73

20090406

17．解：（1） 2分

4分

6分

（2）

根據正弦函數的圖象可得：

當時，

取最大值1 8分

當時

10分

即 12分

18．解：先后拋擲兩枚骰子可能出現的情況：（1，1），（1，2），（1，3），…，（1，6）；（2，1）（2，2），（2，3），…，（2，6）；…；（6，1），（6，2），（6，3），…，（6，6），基本事件總數為36。 2分

（1）在上述基本事件中，“點數之和等于3”的事件只有（1，2），（2，1）兩個可能，點數之和等于2的只有（1，1）一個可能的結果，記點數之和不大于3為事件A₁，則事件A₁發生的概率為： 4分

事件“出現的點數之和大于3”發生的概率為

7分

（2）與（1）類似，在上述基本事件中，“點數之積是3的倍數”的事件有20個可能的結果。

所以事件“出現的點數之積是3的倍數”發生的概率為

12分

BCD是等邊三角形，

E是CD的中點，

而AB//CD， 2分

又平面ABCD，

而呵呵平面PAB。 4分

又平面PAB。 6分

（2）由（1）知，平面PAB，所以

又是二面角A―BE―P的平面角 9分

平面ABCD，

在

故二面角A―BE―P的大小是 12分

20．解：（1）

是首項為的等比數列 2分

4分

當仍滿足上式。

注：未考慮的情況，扣1分。

（2）由（1）得，當時，

8分

兩式作差得

12分

21．解：（1）因為且AB通過原點（0，0），所以AB所在直線的方程為

由得A、B兩點坐標分別是A（1，1），B（-1，-1）。

又的距離。

4分

（2）設AB所在直線的方程為

由

因為A，B兩點在橢圓上，所以

即 5分

設A，B兩點坐標分別為，則

且 6分

8分

又的距離，

即 10分

邊最長。（顯然）

所以AB所在直線的方程為 12分

22．解：（1）

當

令 3分

當的變化情況如下表：

0

2

-

0

+

0

-

0

+

單調遞減

極小值

單調遞增

極大值

單調遞減

極小值

單調遞增

所以上是增函數，

在區間上是減函數 6分

（2）的根。

處有極值。

則方程有兩個相等的實根或無實根，

8分

解此不等式，得

這時，是唯一極值。

因此滿足條件的 10分

注：若未考慮進而得到，扣2分。

（3）由（2）知，當恒成立。

當上是減函數，

因此函數 12分

又上恒成立。

于是上恒成立。

因此滿足條件的 14分

同步練習冊答案

國際學校優選 - 練習冊列表 - 試題列表

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區

違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
版權聲明：本站所有文章，圖片來源于網絡，著作權及版權歸原作者所有，轉載無意侵犯版權，如有侵權，請作者速來函告知，我們將盡快處理，聯系qq：3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號

練習冊

高中

初中

小學