
題目列表(包括答案和解析)
(本小題滿分12分)在一個不透明的盒子中,放有標號分別為1,2,3的三個大小相同的小球,現(xiàn)從這個盒子中,有放回地先后取得兩個小球,其標號分別為![]() ,記
,記![]() . (1)求隨機變量
. (1)求隨機變量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
(本小題滿分12分)
在一個盒子中,放有標號分別為1,2,3的三張卡片,現(xiàn)從這個盒子中,有放回地先后抽得兩張卡片的標號分別為![]() 、
、![]() ,設(shè)
,設(shè)![]() 為坐標原點,點
為坐標原點,點![]() 的坐標為
的坐標為![]() ,記
,記![]() .
.
(I)求隨機變量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(II)求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
(本小題滿分12分)
在一個盒子中放有標號分別為1、2、3的三張卡片,現(xiàn)從這個盒子中有放回地先后抽取兩張卡片,并記它們的標號分別為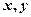 ,設(shè)
,設(shè)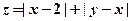 ,
,
(1)求事件“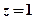 ”發(fā)生的概
”發(fā)生的概 率;
率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
(本小題滿分12分)
一個口袋中裝有大小相同的 個紅球(
個紅球( 且
且 )和
)和 個白球,一次摸獎從中摸兩個球,兩個球的顏色不同則為中獎。
個白球,一次摸獎從中摸兩個球,兩個球的顏色不同則為中獎。
(Ⅰ)試用 表示一次摸獎中獎的概率
表示一次摸獎中獎的概率 ;
;
(Ⅱ)記從口袋中三次摸獎(每次摸獎后放回)恰有一次中獎的概率為 ,求
,求 的最大值?
的最大值?
(Ⅲ)在(Ⅱ)的條件下,將 個白球全部取出后,對剩下的
個白球全部取出后,對剩下的 個紅球全部作如下標記:記上
個紅球全部作如下標記:記上 號的有
號的有 個(
個( ),其余的紅球記上
),其余的紅球記上 號,現(xiàn)從袋中任取一球。
號,現(xiàn)從袋中任取一球。 表示所取球的標號,求
表示所取球的標號,求 的分布列、期望和方差。
的分布列、期望和方差。
(本小題滿分12分)
在一個盒子中放有標號分別為1、2、3的三張卡片,現(xiàn)從這個盒子中有放回地先后抽取兩張卡片,并記它們的標號分別為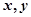 ,設(shè)
,設(shè) ,
,
(1)求事件“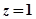 ”發(fā)生的概率;
”發(fā)生的概率;
(2)求 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率。
取得最大值”的概率。
1~10:C C B C A B A B D A
11、學.files/image208.gif) 12、
12、學.files/image210.gif) 13、
13、 學.files/image212.gif) 14、>
14、>
15、學.files/image214.gif) (提示:15.
(提示:15.學.files/image216.gif) ,又
,又學.files/image218.gif)
學.files/image220.gif) )
)
16.解:(1)學.files/image222.gif)
學.files/image224.gif) ………3(分)
………3(分)
由學.files/image226.gif) =0即
=0即學.files/image228.gif)
即對稱中心為學.files/image230.gif) …………6(分)
…………6(分)
(2)已知b2=ac
學.files/image232.gif)
即學.files/image234.gif) 的值域為
的值域為學.files/image236.gif) 綜上所述,
綜上所述,學.files/image238.gif) ,故
,故學.files/image234.gif) 值域為
值域為學.files/image236.gif) …12(分)
…12(分)
17.解:(1)學.files/image240.gif) 的最大值為6,此時有
的最大值為6,此時有學.files/image242.gif) 或
或學.files/image244.gif) ,故所求的概率為
,故所求的概率為
學.files/image246.gif) .
…………5(分)
.
…………5(分)
(2)學.files/image168.gif) 的所有可能取值是0,1,2,3,4,5,6.其分布列為:
的所有可能取值是0,1,2,3,4,5,6.其分布列為:
學.files/image168.gif)
0
1
2
3
4
5
6
學.files/image250.gif)
學.files/image252.gif)
學.files/image254.gif)
學.files/image256.gif)
學.files/image254.gif)
學.files/image254.gif)
學.files/image258.gif)
學.files/image258.gif)
……………10(分)
學.files/image260.gif) ……12(分)
……12(分)
18.解:(1)學.files/image262.gif)
學.files/image264.gif) ,
又
,
又學.files/image266.gif)
學.files/image268.gif)
學.files/image270.gif) …………5(分)
…………5(分)
(2)當學.files/image180.gif) 時,則
時,則學.files/image182.gif)
學.files/image274.gif)
學.files/image276.gif)
其表面積學.files/image278.gif)
當學.files/image280.gif) 與
與學.files/image282.gif) 不垂直時,則
不垂直時,則學.files/image284.gif) ,否則由(1)知
,否則由(1)知學.files/image182.gif) ,可得
,可得學.files/image180.gif) (矛盾).
(矛盾).
當學.files/image288.gif) 時,
時,學.files/image290.gif) 與
與學.files/image292.gif) 不能垂直,否則
不能垂直,否則學.files/image294.gif)
學.files/image296.gif) ,從而
,從而學.files/image298.gif) ,與
,與學.files/image172.gif) 矛盾.
矛盾.
學.files/image301.gif) ,從而可得
,從而可得學.files/image303.gif) …………①
…………①
由學.files/image288.gif) 得,
得,學.files/image306.gif) …………②
…………②
根據(jù)①、②得:學.files/image308.gif) ,從而導致
,從而導致學.files/image310.gif) 矛盾.
矛盾.
學.files/image312.gif) ,從而得到
,從而得到學.files/image314.gif)
當學.files/image284.gif) 時,
時,學.files/image317.gif)
當學.files/image314.gif) 時,
時,學.files/image320.gif)
學.files/image322.gif) ,即四面體的各個面是全等的三角形.
,即四面體的各個面是全等的三角形.
學.files/image324.gif) 其表面積為
其表面積為學.files/image326.gif) .
……………12(分)
.
……………12(分)
19.解:(I)從第n年初到第n+1年初,魚群的繁殖量為axn,被捕撈量為bxn,死亡量為
學.files/image328.gif)
學.files/image330.gif) …………(3分)
…………(3分)
(II)若每年年初魚群總量保持不變,則xn恒等于x1, n∈N*,從而由(*)式得
學.files/image332.gif) 因為x1>0,所以a>b.
因為x1>0,所以a>b.
猜測:當且僅當a>b,且學.files/image334.gif) 時,每年年初魚群的總量保持不變.
……(6分)
時,每年年初魚群的總量保持不變.
……(6分)
(Ⅲ)若b的值使得xn>0,n∈N*, 由xn+1=xn(3-b-xn), n∈N*, 知0<xn<3-b, n∈N*, 特別地,有0<x1<3-b. 即0<b<3-x1,而x1∈(0, 2),所以學.files/image336.gif)
由此猜測b的最大允許值是1. ……………(10分)
下證 當x1∈(0, 2) ,b=1時,都有xn∈(0, 2), n∈N*
①當n=1時,結(jié)論顯然成立.
②假設(shè)當n=k時結(jié)論成立,即xk∈(0, 2),則當n=k+1時,xk+1=xk(2-xk)>0.
又因為xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,所以xk+1∈(0, 2),故當n=k+1時結(jié)論也成立.
由①、②可知,對于任意的n∈N*,都有xn∈(0,2).
綜上所述,為保證對任意x1∈(0, 2), 都有xn>0, n∈N*,則捕撈強度b最大允許值是1.…(13分)
20. 解:(1)設(shè)雙曲線方程為學.files/image338.gif) ,由橢圓
,由橢圓學.files/image184.gif) 求得兩焦點為
求得兩焦點為學.files/image341.gif) ,
,
學.files/image324.gif) 對于雙曲線
對于雙曲線學.files/image344.gif) ,又
,又學.files/image346.gif) 為雙曲線
為雙曲線學.files/image348.gif) 的一條漸近線
的一條漸近線
學.files/image324.gif)
學.files/image350.gif) 解得
解得 學.files/image352.gif) ,
,
學.files/image354.jpg)
學.files/image324.gif) 雙曲線
雙曲線學.files/image348.gif) 的方程為
的方程為學.files/image357.gif) ……………(5分)
……………(5分)
(2)解法一:
由題意知直線學.files/image188.gif) 的斜率
的斜率學.files/image360.gif) 存在且不等于零。
存在且不等于零。
設(shè)學.files/image188.gif) 的方程:
的方程:學.files/image362.gif) ,
,學.files/image364.gif) 則
則學.files/image366.gif)
學.files/image368.gif)
學.files/image370.gif)
學.files/image372.gif)
學.files/image374.gif)
學.files/image376.gif) 在雙曲線
在雙曲線學.files/image348.gif) 上,
上,學.files/image324.gif)
學.files/image380.gif)
學.files/image324.gif)
學.files/image382.gif)
學.files/image324.gif)
學.files/image384.gif)
同理有:學.files/image386.gif)
若學.files/image388.gif) 則直線
則直線學.files/image188.gif) 過頂點,不合題意.
過頂點,不合題意.學.files/image391.gif)
學.files/image393.gif) 是二次方程
是二次方程學.files/image395.gif) 的兩根.
的兩根.
學.files/image397.gif)
學.files/image399.gif) ,
,
此時學.files/image401.gif) .
.學.files/image324.gif) 所求
所求學.files/image403.gif) 的坐標為
的坐標為學.files/image405.gif) .
…………(13分)
.
…………(13分)
解法二:由題意知直線學.files/image188.gif) 的斜率
的斜率學.files/image360.gif) 存在且不等于零
存在且不等于零
設(shè)學.files/image188.gif) 的方程:
的方程:學.files/image410.gif) ,則
,則學.files/image366.gif) .
.
學.files/image413.gif) ,
,學.files/image415.gif) .
.
學.files/image417.gif) ,
,學.files/image419.gif) ,
,學.files/image421.gif) ,
,
又學.files/image423.gif) ,
,學.files/image425.gif) ,即
,即學.files/image427.gif)
將學.files/image429.gif) 代入
代入學.files/image357.gif) 得
得學.files/image432.gif)
學.files/image434.gif) ,否則
,否則學.files/image188.gif) 與漸近線平行。
與漸近線平行。學.files/image437.gif) 。
。
學.files/image439.gif)
學.files/image441.gif)
學.files/image443.gif) .
.
21.(1)學.files/image445.gif)
學.files/image447.gif)
故學.files/image103.gif) 在
在學.files/image450.gif) 上是單調(diào)遞增函數(shù),在
上是單調(diào)遞增函數(shù),在學.files/image452.gif) 上是單調(diào)遞減函數(shù)
……4(分)
上是單調(diào)遞減函數(shù)
……4(分)
(2)①學.files/image454.gif)
學.files/image456.gif)
學.files/image458.gif)
學.files/image460.gif) 是公差為1的等差數(shù)列,且首項為
是公差為1的等差數(shù)列,且首項為學.files/image462.gif)
故學.files/image464.gif)
學.files/image466.gif) ……………9(分)
……………9(分)
②由(1)知,當學.files/image468.gif) 時,
時,學.files/image470.gif) 在
在學.files/image472.gif) 是單調(diào)遞減函數(shù),又
是單調(diào)遞減函數(shù),又學.files/image474.gif) ,
,學.files/image476.gif) ,即
,即學.files/image478.gif)
學.files/image480.gif) .
.
學.files/image482.gif)
學.files/image484.gif)
學.files/image486.gif) ………13(分)
………13(分)
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com