
題目列表(包括答案和解析)
在正三棱柱![]() 中,
中,![]()
求證:⑴![]() ;
;
(2)求二面角![]() 的正切值。
的正切值。

求證:⑴![]() ;
;
(2)求二面角![]() 的正切值。
的正切值。

(13分) 如圖,直三棱柱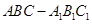 中,
中,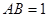 ,
,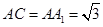 ,
,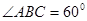 .
.
(Ⅰ)證明: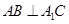 ;
;
(Ⅱ)求二面角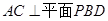
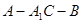 的正切值.
的正切值.
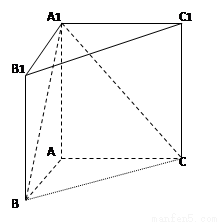
(13分) 如圖,直三棱柱 中,
中,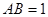 ,
,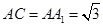 ,
, .
.
(Ⅰ)證明: ;
;
(Ⅱ)求二面角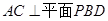
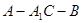 的正切值.
的正切值. 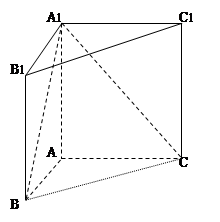
 中,
中, ,
, ,
, .
. ;
;
 的正切值.
的正切值. 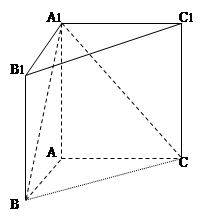
一.選擇題
題號
1
2
3
4
5
6
7
8
9
10
答案
A
D
C
B
B
C
A
C
B
A
二.填空題
11.  12. ② 13.
12. ② 13.  14.
120 15.
14.
120 15. 
三.解答題
16.解:(Ⅰ) . …………………………………3分
. …………………………………3分
由 ,得
,得 .
………………………………5分
.
………………………………5分
(Ⅱ)由(Ⅰ)得 . ………………8分
. ………………8分
由 ,得
,得 .
.
 當
當 ,即
,即 時,函數
時,函數 有最大值
有最大值 . ……………………12分
. ……………………12分
17.解:設此工人一個季度里所得獎金為 ,則
,則 是一個離散型隨機變量.由于該工人每月完成任務與否是等可能的,所以他每月完成任務的概率等于
是一個離散型隨機變量.由于該工人每月完成任務與否是等可能的,所以他每月完成任務的概率等于 . …………………2分
. …………………2分
所以,  ,
, ,
,
 ,
, . …………8分
. …………8分
 于是
于是 .
.
所以此工人在一個季度里所得獎金的期望為153. 75元. ……………………12分
18.解:(Ⅰ)取BC的中點H,連結PH, 連結AH交BD于E.
 . ……………………………2分
. ……………………………2分
又面 面
面 ,
, 面
面 .
.
 ,
, .
.
 ,
, .
.
 ,即
,即 . ………………………………………………4分
. ………………………………………………4分
因為AH為PA在平面 上的射影,
上的射影, . ……………………………6分
. ……………………………6分
(Ⅱ)連結PE,則由(Ⅰ)知 .
.
 為所求二面角的平面角. ……………………………………………8分
為所求二面角的平面角. ……………………………………………8分
在 中,由
中,由 ,求得
,求得 .
.
 .
.
即所求二面角的正切值為 . …………………………………………………12分
. …………………………………………………12分
另解:(Ⅰ)建系設點正確2分,求出兩個法向量2分,判斷正確2分;
(Ⅱ)求出兩個法向量3分,求出余弦值2分,求出正切值1分.
19. 解:(Ⅰ)設 ,則
,則
 ,
,
 .
.
即點C的軌跡方程為 . …………………………………………………3分
. …………………………………………………3分
(Ⅱ) 由題意
由題意 .
.
 . ……………5分
. ……………5分
 .
.
 ,
,
 . ……………………………8分
. ……………………………8分
(Ⅲ) .
. .
.
 .
.
∴雙曲線實軸長的取值范圍是 . ………………………………………………12分
. ………………………………………………12分
20.解: (Ⅰ)由已知得 的定義域為
的定義域為 ,
, . ………………2分
. ………………2分
由題意得 對一切
對一切 恒成立,
恒成立,
 ……………………………………………5分
……………………………………………5分
當 時,
時, ,
,
 .故
.故 .
…………………………………………7分
.
…………………………………………7分
(Ⅱ)假設存在正實數 ,使得
,使得 成立.
成立.
 .
…………………9分
.
…………………9分
由 ,得
,得 ,
, .由于
.由于 ,故應舍去.
,故應舍去.
當 時,
時, ………………………………………11分
………………………………………11分
令 ,解得
,解得 或
或 . …………………………13分
. …………………………13分
另解: 假設存在正實數 ,使得
,使得 成立.
成立.
設 ,則
,則 . ………………………9分
. ………………………9分
由 ,解得
,解得 或
或 .
.
因為 ,
, 在
在 上單調遞增,在
上單調遞增,在 上單調遞減.
上單調遞減.
 . … ……………………………………11分
. … ……………………………………11分
令 ,解得
,解得 或
或 . …………………………13分
. …………………………13分
21.解:(Ⅰ)由已知 ,得
,得 .
.
則數列 是公比為2的等比數列. ……………………………………………2分
是公比為2的等比數列. ……………………………………………2分
又 . ……………………………………………4分
. ……………………………………………4分
(Ⅱ) . …………………6分
. …………………6分
 恒成立,則
恒成立,則


 解得
解得
故存在常數A,B,C,滿足條件. …………………………………………9分
(Ⅲ)由(Ⅱ)知:


 . …………………14分
. …………………14分
=
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com