久操免费在线视频,欧美理论电影在线精品,91精品国产91久久久久福利

3．過程與方法展示函數圖象.讓學生通過觀察.進而研究指數函數的性質. 【查看更多】

題目列表(包括答案和解析)

（Ⅰ）已知：,,求的值;

（Ⅱ）類比（Ⅰ）的過程與方法，將（Ⅰ）中已知條件中兩個等式的左邊進行適當改變，寫出改變后的式子，并求的值.

已知向量p＝(a，x＋1)，q＝(x，a)，m＝(1，y)，且(p－q)∥m，y與x的函數關系式為y＝f(x)．

(1)求f(x)；

(2)判斷并證明函數y＝f(x)當x＞a時的單調性；

(3)我們利用函數y＝f(x)構造一個數列{x_n)，方法如下：對于f(x)定義域中的x₁，令x₂＝f(x₁)，x₃＝f(x₂)，…，x_n＝f(x_n－1)，…．在上述構造數列的過程中，如果x_i(i＝1，2，3，4，…)在定義域中，構造數列的過程將繼續下去；如果x_i不在定義域中，則構造數列的過程停止．如果取f(x)定義域中任一值作為x₁，都可以用上述方法構造出一個無窮數列{x_n}，求實數a的值．

查看答案和解析>>

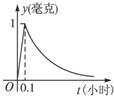為了預防流感，某學校對教室用藥熏消毒法進行消毒．已知藥物釋放過程中，室內每立方米空氣中的含藥量y（毫克）與時間t（小時）成正比；藥物釋放完畢后，y與t的函數關系式為y=（

）^t-a（a為常數），如如圖所示，根據圖中提供的信息，回答下列問題：從藥物釋放開始，每立方米空氣中的含藥量y（毫克）與時間t（小時）之間的函數關系式為

．

查看答案和解析>>

（2011•奉賢區二模）用2π平方米的材料制成一個有蓋的圓錐形容器，如果在制作過程中材料無損耗，且材料的厚度忽略不計，底面半徑長為x，圓錐母線的長為y
（1）建立y與x的函數關系式，并寫出x的取值范圍；
（2）圓錐的母線與底面所成的角大小為

，求所制作的圓錐形容器容積多少立方米（精確到0.01m³）

查看答案和解析>>

某中學，由于不斷深化教育改革，辦學質量逐年提高．2006年至2009年高考考入一流大學人數如下：

年份	2006	2007	2008	2009
高考上線人數	116	172	220	260

以年份為橫坐標，當年高考上線人數為縱坐標建立直角坐標系，由所給數據描點作圖（如圖所示），從圖中可清楚地看到這些點基本上分布在一條直線附近，因此，用一次函數y=ax+b來模擬高考上線人數與年份的函數關系，并以此來預測2010年高考一本上線人數．如下表：

年份	2006	2007	2008	2009
年份代碼x	1	2	3	4
實際上線人數	116	172	220	260
模擬上線人數	y₁=a+b	y₂=2a+b	y₃=3a+b	y₄=4a+b

為使模擬更逼近原始數據，用下列方法來確定模擬函數．
設S=（y₁-y₁′）²+（y₂-y₂′）²+（y₃-y₃′）²+（y₄-y₄′）²，y₁′、y₂′、y₃′、y₄′表示各年實際上線人數，y₁、y₂、y₃、y₄表示模擬上線人數，當S最小時，模擬函數最為理想．試根據所給數據，預測2010年高考上線人數．

查看答案和解析>>

同步練習冊答案

練習冊

高中

初中

小學