
題目列表(包括答案和解析)
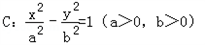 相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3).
相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3).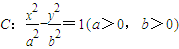 相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3).
相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3). 相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3).
相交于B、D兩點(diǎn),且BD的中點(diǎn)為M(1,3).
一.選擇題:本大題共12小題,每小題5分,共60分。
(1)A (2)B (3)B (4)A (5)D (6)D
(7)C (8)C (9)A (10)C (11)A (12)B
二.填空題:本大題共4小題,每小題5分,共20分。
(13)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image306.gif) (14)2
(15)
(14)2
(15)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image308.gif) (16)44
(16)44
三.解答題:本大題共6小題,共70分,解答應(yīng)寫出文字說(shuō)明,證明過(guò)程或演算步驟。
(17)(本小題滿分10分)
(Ⅰ)解法一:由正弦定理得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image310.gif) .
.
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image312.gif) ,
,
又 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image314.gif) ,
,
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image316.gif) ,
,
即 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image318.gif) ,
,
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image320.gif) .
.
因?yàn)? 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image322.gif) ,
,
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image324.gif) ,
,
又 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image273.gif) 為三角形的內(nèi)角,
為三角形的內(nèi)角,
所以 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image327.gif) . ………………………5分
. ………………………5分
解法二:由余弦定理得 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image329.gif) .
.
將上式代入習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image217.gif) 整理得
整理得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image332.gif) .
.
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image324.gif) ,
,
又 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image273.gif) 為三角形內(nèi)角,
為三角形內(nèi)角,
所以 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image327.gif) .
………………………5分
.
………………………5分
(Ⅱ)解:因?yàn)?sub>習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image335.gif) .
.
故 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image337.gif) ,
,
由已知 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image221.gif) 得
得
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image340.gif)
又因?yàn)?nbsp; 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image342.gif) .
.
得 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image344.gif) ,
,
所以 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image346.gif) ,
,
解得 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image348.gif) . ………………………………………………10分
. ………………………………………………10分
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image236.jpg) (18)(本小題滿分12分)
(18)(本小題滿分12分)
(Ⅰ)證明:
∵習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image227.gif) 面
面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image225.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image350.gif) 面
面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image225.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image353.gif) .
.
又∵底面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image225.gif) 是正方形,
是正方形,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image355.gif) .
.
又∵習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image357.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image359.gif) 面
面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image234.gif) ,
,
又∵習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image350.gif) 面
面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image363.gif) ,
,
∴平面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image230.gif)
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image232.gif) 平面
平面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image234.gif) . ………………………………………6分
. ………………………………………6分
(Ⅱ)解法一:如圖建立空間直角坐標(biāo)系習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image365.gif) .
.
設(shè)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image367.gif) ,則
,則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image369.gif) ,在
,在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image371.gif) 中,
中,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image373.gif) .
.
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image375.gif) 、
、習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image377.gif) 、
、習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image379.gif) 、
、習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image381.gif) 、
、習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image383.gif) 、
、習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image385.gif) .
.
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image386.gif) ∵
∵習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image141.gif) 為
為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image241.gif) 的中點(diǎn),
的中點(diǎn),習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image388.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image390.gif) .
.
設(shè)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image392.gif) 是平面
是平面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image394.gif) 的一個(gè)法向量.
的一個(gè)法向量.
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image396.gif) 則由
則由習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image398.gif) 可求得
可求得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image400.gif) .
.
由(Ⅰ)知習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image402.gif) 是平面
是平面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image234.gif) 的一個(gè)法向量,
的一個(gè)法向量,
且習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image405.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image407.gif) ,即
,即習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image409.gif) .
.
∴二面角習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image243.gif) 的大小為
的大小為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image411.gif) . ………………………………………12分
. ………………………………………12分
解法二:
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image413.jpg) 設(shè)
設(shè)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image367.gif) ,則
,則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image369.gif) ,
,
在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image371.gif) 中,
中,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image373.gif) .
.
設(shè)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image415.gif) ,連接
,連接習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image417.gif) ,過(guò)
,過(guò)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image163.gif) 作
作習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image420.gif) 于
于習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image422.gif) ,
,
連結(jié)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image424.gif) ,由(Ⅰ)知
,由(Ⅰ)知習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image426.gif) 面
面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image428.gif) .
.
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image424.gif) 在面
在面習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image428.gif) 上的射影為
上的射影為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image431.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image433.gif) .
.
故習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image435.gif) 為二面角
為二面角習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image437.gif) 的平面角.
的平面角.
在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image439.gif) 中,
中,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image441.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image443.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image445.gif) .
.
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image447.gif) ,
,
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image449.gif) .
.
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image451.gif) .
.
即二面角習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image243.gif) 的大小為
的大小為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image411.gif) . …………………………………12分
. …………………………………12分
(19)(本小題滿分12分)
解:(Ⅰ)設(shè)取到的4個(gè)球全是白球的概率習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image298.gif) ,
,
則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image454.gif) .
…………………………………6分
.
…………………………………6分
(Ⅱ)設(shè)取到的4個(gè)球中紅球個(gè)數(shù)不少于白球個(gè)數(shù)的概率習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image456.gif) ,
,
則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image458.gif) . ………………12分
. ………………12分
(20)(本小題滿分12分)
解:(I)設(shè)等比數(shù)列習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image245.gif) 的首項(xiàng)為
的首項(xiàng)為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image460.gif) ,公比為
,公比為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image462.gif) ,
,
依題意,有習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image464.gif) ,
,
代入習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image247.gif) , 得
, 得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image466.gif) .
.
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image468.gif) .
…………………………………2分
.
…………………………………2分
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image470.gif) 解之得
解之得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image472.gif) 或
或習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image474.gif) …………………6分
…………………6分
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image476.gif) 或
或習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image478.gif) .
…………………………………8分
.
…………………………………8分
(II)又習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image480.gif) 單調(diào)遞減,∴
單調(diào)遞減,∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image474.gif) . …………………………………9分
. …………………………………9分
則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image482.gif) . …………………………………10分
. …………………………………10分
∴習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image484.gif) ,即
,即習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image486.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image488.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image490.gif) .
.
故使習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image492.gif) 成立的正整數(shù)n的最小值為8.………………………12分
成立的正整數(shù)n的最小值為8.………………………12分
(21)(本小題滿分12分)
(Ⅰ)解:設(shè)雙曲線方程為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image494.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image496.gif) ,
,
由習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image266.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image268.gif) 及勾股定理得
及勾股定理得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image498.gif) ,
,
由雙曲線定義得 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image500.gif) .
.
則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image502.gif) .
………………………………………5分
.
………………………………………5分
(Ⅱ)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image504.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image506.gif)
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image508.gif) ,雙曲線的兩漸近線方程為
,雙曲線的兩漸近線方程為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image510.gif) .
.
由題意,設(shè)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image167.gif) 的方程為
的方程為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image512.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image167.gif) 與
與習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image514.gif) 軸的交點(diǎn)為
軸的交點(diǎn)為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image516.gif) .
.
若習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image167.gif) 與
與習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image518.gif) 交于點(diǎn)
交于點(diǎn)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image271.gif) ,
,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image167.gif) 與
與習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image521.gif) 交于點(diǎn)
交于點(diǎn)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image273.gif) ,
,
由習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image524.gif) 得
得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image526.gif) ;由
;由習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image528.gif) 得
得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image530.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image532.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image534.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image536.gif) 則
則習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image538.gif) ,
,
故雙曲線方程為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image540.gif) .
………………………………12分
.
………………………………12分
(22)(本小題滿分12分)
解:(Ⅰ)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image542.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image544.gif) .
.
又因?yàn)楹瘮?shù)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image283.gif) 在
在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image285.gif) 上為增函數(shù),
上為增函數(shù),
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image546.gif) 在
在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image285.gif) 上恒成立,等價(jià)于
上恒成立,等價(jià)于
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image548.gif) 在
在習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image285.gif) 上恒成立.
上恒成立.
又習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image550.gif) ,
,
故當(dāng)且僅當(dāng)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image552.gif) 時(shí)取等號(hào),而
時(shí)取等號(hào),而習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image554.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image556.gif) 的最小值為
的最小值為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image558.gif) .
………………………………………6分
.
………………………………………6分
(Ⅱ)由已知得:函數(shù)習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image279.gif) 為奇函數(shù),
為奇函數(shù),
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image560.gif) ,
, 習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image562.gif) , ………………………………7分
, ………………………………7分
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image564.gif) .
.
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image566.gif) 切點(diǎn)為
切點(diǎn)為習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image568.gif) ,其中
,其中習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image570.gif) ,
,
則切線習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image167.gif) 的方程為:
的方程為:習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image572.gif) ……………………8分
……………………8分
由習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image574.gif) ,
,
得習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image576.gif) .
.
又習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image578.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image580.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image582.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image584.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image586.gif) 或
或習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image588.gif) ,由題意知,
,由題意知,習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image590.gif)
從而習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image592.gif) .
.
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image594.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image596.gif) ,
,
習(xí)適應(yīng)性檢測(cè)(數(shù)學(xué)文).files/image598.gif) .
………………………………………12分
.
………………………………………12分
本資料由《七彩教育網(wǎng)》www.7caiedu.cn 提供!
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com