
題目列表(包括答案和解析)
在△ABC中,a、b、c分別是角A、B、C的對邊,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面積.
,BC=5,求△ABC的面積.
【解析】第一問中sinB=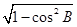 =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二問中,由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
+25-8AB
解得AB=5或AB=3綜合得△ABC的面積為 或
或
解:⑴ sinB=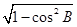 =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,則S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
= ………………10分
………………10分
若AB=3,則S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
綜合得△ABC的面積為 或
或
已知冪函數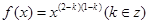 滿足
滿足 。
。
(1)求實數k的值,并寫出相應的函數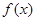 的解析式;
的解析式;
(2)對于(1)中的函數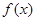 ,試判斷是否存在正數m,使函數
,試判斷是否存在正數m,使函數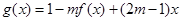 ,在區間上的最大值為5。若存在,求出m的值;若不存在,請說明理由。
,在區間上的最大值為5。若存在,求出m的值;若不存在,請說明理由。
【解析】本試題主要考查了函數的解析式的求解和函數的最值的運用。第一問中利用,冪函數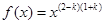 滿足
滿足 ,得到
,得到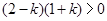
因為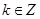 ,所以k=0,或k=1,故解析式為
,所以k=0,或k=1,故解析式為
(2)由(1)知,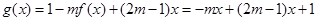 ,
, ,因此拋物線開口向下,對稱軸方程為:
,因此拋物線開口向下,對稱軸方程為: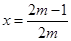 ,結合二次函數的對稱軸,和開口求解最大值為5.,得到
,結合二次函數的對稱軸,和開口求解最大值為5.,得到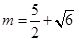
(1)對于冪函數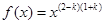 滿足
滿足 ,
,
因此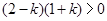 ,解得
,解得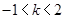 ,………………3分
,………………3分
因為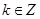 ,所以k=0,或k=1,當k=0時,
,所以k=0,或k=1,當k=0時, ,
,
當k=1時, ,綜上所述,k的值為0或1,
,綜上所述,k的值為0或1, 。………………6分
。………………6分
(2)函數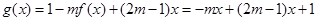 ,………………7分
,………………7分
由此要求 ,因此拋物線開口向下,對稱軸方程為:
,因此拋物線開口向下,對稱軸方程為: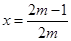 ,
,
當 時,
時,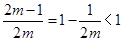 ,因為在區間
,因為在區間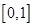 上的最大值為5,
上的最大值為5,
所以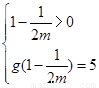 ,或
,或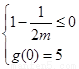 …………………………………………10分
…………………………………………10分
解得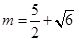 滿足題意
滿足題意
 12、為了考察某種大麥穗長的分布情況,在一塊試驗地里抽取了100個穗,量得它們的長度(單位:cm)之后,將所得數據以0.3cm為組距,分成如下12個組:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通過分析計算,最后畫出的頻數分布直方圖如圖,由圖可知( )
12、為了考察某種大麥穗長的分布情況,在一塊試驗地里抽取了100個穗,量得它們的長度(單位:cm)之后,將所得數據以0.3cm為組距,分成如下12個組:3.95~4.25,4.25~4.55,4.55~4.85,…,6.95~7.25,7.25~7.55,通過分析計算,最后畫出的頻數分布直方圖如圖,由圖可知( )湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com