題目列表(包括答案和解析)
(本小題滿分12分) 甲、乙兩人參加某電視臺舉辦的答題闖關游戲，按照規則，
甲先從
道備選題中一次性抽取
道題獨立作答，然后由乙回答剩余題，每人答對其中
題就停止答題，即闖關成功．已知在道備選題中，甲能答對其中的
道題，乙答對每道題
的概率都是
．
（Ⅰ）求甲、乙至少有一人闖關成功的概率；
（Ⅱ）設甲答對題目的個數為ξ，求ξ的分布列及數學期望．
(本小題滿分12分) 甲、乙兩人參加某電視臺舉辦的答題闖關游戲，按照規則，
甲先從
道備選題中一次性抽取
道題獨立作答，然后由乙回答剩余題，每人答對其中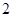
題就停止答題，即闖關成功．已知在道備選題中，甲能答對其中的
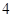道題，乙答對每道題
的概率都是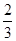
．
（Ⅰ）求甲、乙至少有一人闖關成功的概率；
（Ⅱ）設甲答對題目的個數為ξ，求ξ的分布列及數學期望．
本小題滿分12分)
甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次．記錄如下：
甲：82 81 79 78 95 88 93 84 乙：92 95 80 75 83 80 90 85
（1）畫出甲、乙兩位學生成績的莖葉圖，指出學生乙成績的中位數；
（2）現要從中選派一人參加數學競賽，從平均狀況和方差的角度考慮，你認為派哪位學生參加合適?請說明理由；
（3）若將頻率視為概率，對學生甲在今后的三次數學競賽成績進行預測，記這三次成績中高于80分的次數為
，求的分布列及數學期望
.
(本小題滿分12分)
甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次．記錄如下：
甲：82 81 79 78 95 88 93 84 乙：92 95 80 75 83 80 90 85
（1）畫出甲、乙兩位學生成績的莖葉圖，指出學生乙成績的中位數；
（2）現要從中選派一人參加數學競賽，從平均狀況和方差的角度考慮，你認為派哪位學生參加合適?請說明理由；
（3）若將頻率視為概率，對學生甲在今后的三次數學競賽成績進行預測，記這三次成績中高于80分的次數為
，求的分布列及數學期望
.
( 本小題滿分12分)
甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取8次．記錄如下：
甲：82 81 79 78 95 88 93 84 乙：92 95 80 75 83 80 90 85
（I）畫出甲、乙兩位學生成績的莖葉圖，指出學生乙成績的中位數；
（II）現要從中選派一人參加數學競賽，從平均狀況和方差的角度考慮，你認為派哪位學生參加合適?請說明理由；
（III）若將頻率視為概率，對學生甲在今后的三次數學競賽成績進行預測，記這三次成績中高于80分的次數為
，求的分布列及數學期望
.
一、選擇題 A D B A C B A D A C B B
二、填空題
13.
. 14.
15. 
.16.①②③④
三、解答題
17.(1)
=
=
=
=
=
=
.
∴
的最小正周期
．
(2) ∵
, ∴
.
∴當
,即
=
時,有最大值
;
當
,即=
時,有最小值-1．
18. （1）連結
，則
是的中點，
在△
中，
，
且
平面
，
平面，
∴∥平面
（2） 因為
平面
，
平面,
,
又⊥
，所以，⊥平面
，
∴四邊形 是矩形,
且側面⊥平面
取
的中點
,
,
且
平面.
所以，多面體
的體積
19．解：（Ⅰ）依題意，甲答對試題數
的概率分布如下：
0
1
2
3
甲答對試題數的數學期望：
（Ⅱ）設甲、乙兩人考試合格的事件分別為
則 
甲、乙兩人考試均不合格的概率為：
∴甲、乙兩人至少一個合格的概率為
20.(1)
，
∴ 
，于是
，
∴
為首相和公差均為1的等差數列.
由 
,
得, 
∴
．
(2)
,
,
兩式相減，得
,
解出
21. 因
而函數
在
處取得極值2
所以 
所以 
為所求
（2）由（1）知
可知，的單調增區間是
所以，
所以當
時，函數在區間
上單調遞增
（3）由條件知，過的圖形上一點
的切線
的斜率
為：
令
，則
,
此時 ，
根據二次函數
的圖象性質知：
當
時，
當
時，
所以，直線的斜率的取值范圍是
22. 解：（1）∵點A在圓
，
由橢圓的定義知：|AF1|+|AF2|=2a，
（2）∵函數
∴
點F1（－1，0），F2（1，0），
①若
，
∴
②若AB與x軸不垂直，設直線AB的斜率為k，則AB的方程為y=k（x+1）
由
…………（*）
方程（*）有兩個不同的實根.
設點A（x1，y1），B（x2，y2），則x1，x2是方程（*）的兩個根
由①②知
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com