題目列表(包括答案和解析)
（本小題滿分12分）
某高校設計了一個實驗學科的實驗考查方案：考生從6道備選題中一次性隨機抽取3題，按照題目要求獨立完成全部實驗操作。規定：至少正確完成其中2題的便可提交通過。已知6道備選題中考生甲有4道題能正確完成，2道題不能完成；考生乙每題正確完成的概率都是
，且每題正確完成與否互不影響。
（Ⅰ）分別寫出甲、乙兩考生正確完成題數的概率分布列，并計算數學期望；
（Ⅱ）試從兩位考生正確完成題數的數學期望及至少正確完成2題的概率分析比較兩位考生的實驗操作能力．
（本小題滿分12分）
某高校設計了一個實驗學科的實驗考查方案：考生從6道備選題中一次性隨機抽取3題，按照題目要求獨立完成全部實驗操作。規定：至少正確完成其中2題的便可提交通過。已知6道備選題中考生甲有4道題能正確完成，2道題不能完成；考生乙每題正確完成的概率都是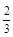
，且每題正確完成與否互不影響。
（Ⅰ）分別寫出甲、乙兩考生正確完成題數的概率分布列，并計算數學期望；
（Ⅱ）試從兩位考生正確完成題數的數學期望及至少正確完成2題的概率分析比較兩位考生的實驗操作能力．
（本小題滿分12分）
道路交通安全法中將飲酒后違法駕駛機動車的行為分成兩個檔次：“酒后駕車”和“醉酒駕車”，其檢測標準是駕駛人員血液中的酒精含量Q（簡稱血酒含量，單位是毫克/100毫升），當20≤Q<80時，為酒后駕車；當Q≥80時，為醉酒駕車．某市公安局交通管理部門在某路段的一次攔查行動中，依法檢查了200輛機動車駕駛員的血酒含量，其中查處酒后駕車的有6人，查處醉酒駕車的有2人，依據上述材料回答下列問題：
（Ⅰ）分別寫出違法駕車發生的頻率和醉酒駕車占違法駕車總數的百分數；
（Ⅱ）從違法駕車的8人中抽取2人，求取到醉酒駕車人數的分布列和期望。
（Ⅲ）飲酒后違法駕駛機動車極
易發生交通事故，假設酒后駕車和醉酒駕車發生交通事故的概率分別是0．1和0．25，且每位駕駛員是否發生交通事故是相互獨立的。依此計算被查處的8名駕駛員中至少有一人發生交通事故的概率（列式）。
（本小題滿分12分）
為了加快經濟的發展，某市選擇A、B兩區作為龍頭帶動周邊地區的發展，決定在A、B兩區的周邊修建城際快速通道，假設A、B兩區相距
個單位距離，城際快速通道所在的曲線為E，使快速通道E上的點到兩區的距離之和為4個單位距離.
（Ⅰ）以線段AB的中點O為原點建立如圖所示的直角坐標系，求城際快速通道所在曲線E的方程；
（Ⅱ）若有一條斜率為
的筆直公路l與曲線E交于P，Q兩點，同時在曲線E上建一個加油站M（橫坐標為負值）滿足
,求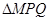
面積的最大值．
（本小題滿分12分）
2012年4月15日，央視《每周質量報告》曝光某省一些廠商用生石灰處理皮革廢料，熬制成工業明膠，賣給一些藥用膠囊生產企業，由于皮革在工業加工時，要使用含鉻的鞣制劑，因此這樣制成的膠囊，往往重金屬鉻超標，嚴重危害服用者的身體健康。該事件報道后，某市藥監局立即成立調查組，要求所有的藥用膠囊在進入市場前必須進行兩輪檢測，只有兩輪都合格才能進行銷售，否則不能銷售，兩輪檢測是否合格相互沒有影響。
（1）某藥用膠囊共生產3個不同批次，經檢測發現有2個批次為合格，另1個批次為不合格，現隨機抽取該藥用膠囊5件，求恰有2件不能銷售的概率；
（2）若對某藥用膠囊的3個不同批次分別進行兩輪檢測，藥品合格的概率如下表：
|
|
第1批次 |
第2批次 |
第3批次 |
|
第一輪檢測 |
|
|
|
|
第二輪檢測 |
|
|
|
記該藥用膠囊能通過檢測進行銷售的批次數為
，求的分布列及數學期望
一．選擇題
序號
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
B
D
D
C
A
A
C
B
D
A
二填空題
13. 2或8； 14．
；
15．
； 16.
.
三．解答題
17．解：（Ⅰ）
………………………………………………………………4分
…………………………6分
（Ⅱ）
…………………………………………………8分
∴
…………………………………………………………………………10分
………………………………………………………………………………12分
18．解：（Ⅰ）在Rt△ABC中，AB＝1，∠BAC＝60°，∴BC＝
，AC＝2．
在Rt△ACD中，AC＝2，∠CAD＝60°，∴CD＝2，AD＝4．
……………………………2分
∴
＝
．………………………………………………………………4分
則V＝
． ……………………………………………………………… 6分
（Ⅱ）∵PA＝CA，F為PC的中點，∴AF⊥PC． ……………………………………8分
∵PA⊥平面ABCD，∴PA⊥CD．
∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC．∴CD⊥PC．
∵E為PD中點，F為PC中點，∴EF∥CD．則EF⊥PC． ………………………………10分
∵AF∩EF＝F，∴PC⊥平面AEF．………………………………………………………………12分
19．設第一個匣子里的三把鑰匙為A，B，C，第二個匣子里的三把鑰匙為a,b,c(設A,a能打開所有門，B只能打開第一道門，b只能打開第二道門，C,c不能打開任何一道門)
（Ⅰ）第一道門打不開的概率為
；……………………………………………………………5分
（Ⅱ）能進入第二道門的情況有Aa,Ab,Ac,Ba,Bb,而二把鑰匙的不同情況有Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc共9種，故能進入第二道門的概率為
……………………………………………………………12分
20.（Ⅰ）依題
即
（
…………………………………………………3分
故
為等差數列，a1=1，d=2
………………………………………………………………………………………………5分
（Ⅱ）設公比為q，則由b1b2b3=8，bn>0
…………………………………………………6分
又
成等差數列
………………………………………………………………………………………8分
或
…………………………………………………………………………………10分
或
……………………………………………………………………12分
21解：（Ⅰ）依題PN為AM的中垂線
…………………………………………………2分
又C（-1，0），A（1，0）
所以N的軌跡E為橢圓，C、A為其焦點…………………………………………………………4分
a=，c=1，所以
為所求………………………………………………………5分
（Ⅱ）設直線
的方程為：y=k（x-1），代入橢圓E的方程：x2+2y2=2得：
（1+2k2）x2-4k2x+2k2-2=0………………（1）
設G（x1，y1）、H（x2，y2），則x1，x2是（1）的兩個根.
…………………………………………………………7分
依題
………………………………………………………9分
解得：
………………………………………………………………………12分
22.解法（一）：
時，
即
……①
⑴
時,
恒成立，
⑵
時，①式化為
……②
⑶
時，①式化為
……③…………………………………………………5分
記
，則
…………………………7分
所以
故由②
，由③
………………………………………………………………………13分
綜上
時，在恒成立.………………………………………………14分
解法（二）：
時， 即……①
⑴
時,
，
，不合題意…………………………………………………2分
⑵
恒成立
∴
在
上為減函數，
得
，矛盾，…………………………………………………………………………………5分
⑶
，
=
若
則
，
，故在［－1,1］內，
，得，矛盾.
若
依題意，
解得
即
綜上為所求.……………………………………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
