題目列表(包括答案和解析)
（本題滿分12）已知
，
．
（Ⅰ）當
時，求證：
在
上是減函數；
（Ⅱ）如果對
不等式
恒成立，求實數
的取值范圍．
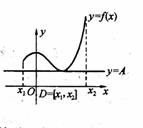（本題滿分12）如右圖所示，定義在D上的函數
，如果滿足：對
，
常數A，都有
成立，則稱函數在D上有下界，其中A稱為函數的下界．（提示：圖中的常數A可以是正數，也可以是負數或零）
（1）試判斷函數
在
上是否有下界？并說明理由；
（2）已知某質點的運動方程為
，要使在
上的每一時刻該質點的瞬時速度是以
為下界的函數，求實數a的取值范圍．
（本題滿分12）已知
是實數，函數
，如果函數
在區間
上有零點，求的取值范圍.
（本題滿分12）
定義在R上的函數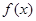
滿足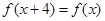
，當2≤x≤6時，
。
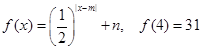（1）求m ，n的值；
（2）比較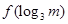
與
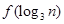的大小
（本題滿分12）
甲、乙兩人各射擊一次，擊中目標的概率分別是
和
。假設兩人射擊是否擊中目標相互之間沒有影響；每人各次射擊是否擊中目標相互之間也沒有影響。
(Ⅰ) 求甲射擊4次，至少有1次未擊中目標的概率；
(Ⅱ) 求兩人各射擊4次，甲恰好擊中目標2次，且乙恰好擊中目標3次的概率；
(Ⅲ) 假設某人連續2次未擊中目標,則終止其射擊,問乙恰好射擊5次后被終止射擊的概率是多少?
一、選擇題（每小題5分，共60 ）
DCAAD BCBAB CB
二、填空題（每小題4分，共16分）
13.100 14.0 15. 
16.B
三、解答題
17.
解
：
（3分）
又
（6分）
(2)
又
18．解：（Ⅰ）擲出點數x可能是：1，2，3，4.
則
分別得：
。于是
的所有取值分別為：0，1，4 .
因此
的所有取值為：0，1，2，4，5，8. …………………………………………2分
當
且
時，
可取得最大值8，
此時，
；
………………………………………………………4分
當
時且
時，可取得最小值 0.
此時
…………………………………………………………6分
（Ⅱ）由（1）知的所有取值為：0，1，2，4，5，8.
……………………………………………………………7分
當
時,
的所有取值為(2，3)、(4，3)、(3，2),(3，4)即
；
當
時,的所有取值為(2，2)、(4，4)、(4，2),(2，4)即
…8分
當
時,的所有取值為(1，3)、(3，1)即
；
當
時,的所有取值為(1，2)、(2，1)、(1，4),(4，1)即
…9分
所以的分布列為：
0
1
2
4
5
8
…
…………10分
即的期望
………………12分
19．（本題12分）
解：（I）連接AO，
D1在底面AC的射影是O，
平面AC，…………2分
AO是AD1在平面AC的射影，
底面ABCD為矩形，
AB=2，AD=1，O是CD的中點，
…………4分
（II）過O作
，連接D
則
是二面角D1―AC―D的平面角。…………6分
平面AC，
與平面AC所成的角，
在
…………8分
（III）過C作
于N，
底面ABCD，底面ABCD是矩形。
平面DD1O，
平面ADD1，…………10分
線段CN的長即C到平面ADD1的距離。…………11分
所以C到平面ADD1的距離是
…………12分
解法二（II）：由（I）知OA、OB、OD1兩兩垂直，以O為坐標原點，直線OA、OB、OD1分別為
軸，建立如圖所示的空間直角坐標系
所以
…………6分
…………8分
…………12分
得a4=
a3=33.同理可得
符合題意，則
必為與n無關的常數
，得
}為等差數列。 ……………………5分
故
……………………12分
，
，
，
，設P
，則
………………………………………3分
，
，即點P為橢圓短軸端點時，
有最小值－2；
，即點P為橢圓長軸端點時，
：
，A（
），B（
）
，消去
，整理得：
，
得：
或
………7分 ①
……………………………………………8分
，即
，∴
……………………..12分
…………2分 又
…………3分
可化為
的變化情況如下表：
…………6分
為偶函數，
時，