
題目列表(包括答案和解析)
意大利數(shù)學家斐波那契(L.Fibonacci)在他的1228年出版的《算經(jīng)》一書中,記述了有趣的兔子問題,假定每對大兔子每月能生一對小兔子,而每對小兔子過了一個月就可以長成大兔子,如果不發(fā)生死亡,那么由一對大兔子開始,一年后能有多少對大兔子呢?若一直推算下去,可得到一個數(shù)列{an}.若a1=a2=1,你能歸納出當n≥3時an的遞推關系嗎?
| 2 | ||
|
| MA |
| MB |
| AB |
本題滿分14分)
已知函數(shù)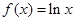 ,
,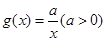 ,設
,設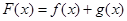 .
.
(Ⅰ)求函數(shù)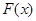 的單調區(qū)間;
的單調區(qū)間;
(Ⅱ)若以函數(shù)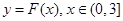 圖像上任意一點
圖像上任意一點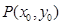 為切點的切線的斜率
為切點的切線的斜率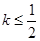 恒成立,求實數(shù)
恒成立,求實數(shù)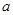 的最小值;
的最小值;
(Ⅲ)是否存在實數(shù)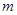 ,使得函數(shù)
,使得函數(shù)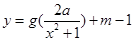 的圖像與函數(shù)
的圖像與函數(shù)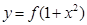 的圖像恰有四個不同的交點?若存在,求出實數(shù)
的圖像恰有四個不同的交點?若存在,求出實數(shù)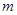 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
(本題滿分為12分)
已知函數(shù) 的圖像過坐標原點
的圖像過坐標原點 ,且在點
,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(1)求實數(shù) 的值;
的值;
(2)求 在區(qū)間
在區(qū)間 上的最大值;
上的最大值;
(3)對任意給定的正實數(shù) ,曲線
,曲線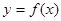 上是否存在兩點
上是否存在兩點 ,使得
,使得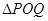 是以
是以 為直角頂點的直角三角形,且此三角形斜邊的中點在軸上?請說明理由.
為直角頂點的直角三角形,且此三角形斜邊的中點在軸上?請說明理由.
(本小題滿分16分) [已知數(shù)列 滿足
滿足
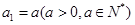 ,
,
 .
.
(1)求數(shù)列 的通項公式
的通項公式 ;
;
(2)若對每一個正整數(shù) ,若將
,若將 按從小到大的順序排列后,此三項均能構成等
按從小到大的順序排列后,此三項均能構成等
差數(shù)列, 且公差為 .①求
.①求 的值及對應的數(shù)列
的值及對應的數(shù)列 .
.
②記 為數(shù)列
為數(shù)列 的前
的前 項和,問是否存在
項和,問是否存在 ,使得
,使得 對任意正整數(shù)
對任意正整數(shù) 恒成立?若存
恒成立?若存
在,求出 的最大值;若不存在,請說明理由.
的最大值;若不存在,請說明理由.
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com