
題目列表(包括答案和解析)
(本題滿分13分)已知 是橢圓
是橢圓 的兩個焦點,
的兩個焦點, 為坐標(biāo)原點,點
為坐標(biāo)原點,點 在橢圓上,且
在橢圓上,且 ,⊙
,⊙ 是以
是以 為直徑的圓,直線
為直徑的圓,直線 :
: 與⊙
與⊙ 相切,并且與橢圓交于不同的兩點
相切,并且與橢圓交于不同的兩點
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)當(dāng) ,且滿足
,且滿足 時,求弦長
時,求弦長 的取值范圍.
的取值范圍.
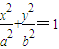 (a>b>0)的一個焦點與拋物線y2=4x的焦點重合,且截拋物線的準(zhǔn)線所得弦長為
(a>b>0)的一個焦點與拋物線y2=4x的焦點重合,且截拋物線的準(zhǔn)線所得弦長為 ,直線l:y=kx+m交橢圓于不同的兩點A,B,且l總與以原點為圓心的單位圓相切.
,直線l:y=kx+m交橢圓于不同的兩點A,B,且l總與以原點為圓心的單位圓相切.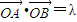 且滿足
且滿足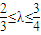 時,求S△AOB的取值范圍.
時,求S△AOB的取值范圍.| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| OA |
| OB |
| OP |
| 3 |
已知橢圓![]() 過定點A(1,0),且焦點在x軸上,橢圓與曲線|y|=x的交點為B、C。現(xiàn)有以A為焦點,過點B、C且開口向左的拋物線,拋物線的頂點坐標(biāo)為M(m,0)。當(dāng)橢圓的離心率e滿足
過定點A(1,0),且焦點在x軸上,橢圓與曲線|y|=x的交點為B、C。現(xiàn)有以A為焦點,過點B、C且開口向左的拋物線,拋物線的頂點坐標(biāo)為M(m,0)。當(dāng)橢圓的離心率e滿足![]() 時,求實數(shù)m的取值范圍。
時,求實數(shù)m的取值范圍。
 +
+ =1(a>b>0)的兩個焦點,O為坐標(biāo)原點,點P(-1,
=1(a>b>0)的兩個焦點,O為坐標(biāo)原點,點P(-1, )在橢圓上,且
)在橢圓上,且 •
• =0,⊙O是以F1F2為直徑的圓,直線l:y=kx+m與⊙O相切,并且與橢圓交于不同的兩點A,B
=0,⊙O是以F1F2為直徑的圓,直線l:y=kx+m與⊙O相切,并且與橢圓交于不同的兩點A,B •
•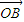 =λ,且滿足
=λ,且滿足 ≤λ≤
≤λ≤ 時,求弦長|AB|的取值范圍.
時,求弦長|AB|的取值范圍.
1.B 2 D. 3.B 4.C 5.C 6.C 7.B 8.C 9.D 10.B
11.D 12.B
13.240 14.1 15.學(xué)文科.files/image243.gif) 16.
①②③
16.
①②③
17.(本題滿分10分)
解:(Ⅰ)由學(xué)文科.files/image245.gif)
學(xué)文科.files/image247.gif) 又
又學(xué)文科.files/image249.gif)
學(xué)文科.files/image251.gif)
(Ⅱ)學(xué)文科.files/image253.gif)
學(xué)文科.files/image255.gif)
同理:學(xué)文科.files/image257.gif)
學(xué)文科.files/image259.gif)
學(xué)文科.files/image261.gif)
學(xué)文科.files/image263.gif)
故學(xué)文科.files/image265.gif) ,
,學(xué)文科.files/image267.gif) ,
,學(xué)文科.files/image269.gif) .
.
18.(本題滿分12分)
解:(Ⅰ)記“這批太空種子中的某一粒種子既發(fā)芽又發(fā)生基因突變”為事件學(xué)文科.files/image098.gif) ,則
,則學(xué)文科.files/image272.gif) .
.
(Ⅱ) 學(xué)文科.files/image274.gif)
19.(本題滿分12分)
解學(xué)文科.files/image276.gif) (Ⅰ)∵
(Ⅰ)∵學(xué)文科.files/image278.gif) ,∴{
,∴{學(xué)文科.files/image280.gif) }是公差為4的等差數(shù)列,
}是公差為4的等差數(shù)列,
∵a1=1, 學(xué)文科.files/image280.gif) =
=學(xué)文科.files/image282.gif) +4(n-1)=4n-3,∵an>0,∴an=
+4(n-1)=4n-3,∵an>0,∴an=學(xué)文科.files/image284.gif)
(Ⅱ)bn=Sn+1-Sn=an+12=學(xué)文科.files/image286.gif) ,由bn<
,由bn<學(xué)文科.files/image288.gif) ,得m>
,得m>學(xué)文科.files/image290.gif) ,
,
設(shè)g(n)= 學(xué)文科.files/image290.gif) ,∵g(n)=
,∵g(n)= 學(xué)文科.files/image290.gif) 在n∈N*上是減函數(shù),
在n∈N*上是減函數(shù),
∴g(n)的最大值是g(1)=5,
∴m>5,存在最小正整數(shù)m=6,使對任意n∈N*有bn<學(xué)文科.files/image288.gif) 成立
成立
20.(本題滿分12分)
解法一:
(I)設(shè)學(xué)文科.files/image067.gif) 是
是學(xué)文科.files/image294.gif) 的中點,連結(jié)
的中點,連結(jié)學(xué)文科.files/image296.gif) ,則四邊形
,則四邊形學(xué)文科.files/image298.gif) 為正方形,
為正方形,
學(xué)文科.files/image300.gif) .故
.故學(xué)文科.files/image302.gif) ,
,學(xué)文科.files/image304.gif) ,
,學(xué)文科.files/image306.gif) ,
,學(xué)文科.files/image308.gif) ,即
,即學(xué)文科.files/image310.gif) .
.
學(xué)文科.files/image311.gif) 又
又學(xué)文科.files/image313.gif) ,
,學(xué)文科.files/image315.gif)
學(xué)文科.files/image317.gif) 平面
平面學(xué)文科.files/image319.gif) ,
,
(II)由(I)知學(xué)文科.files/image199.gif) 平面
平面學(xué)文科.files/image319.gif) ,
,
又學(xué)文科.files/image321.gif) 平面
平面學(xué)文科.files/image319.gif) ,
,學(xué)文科.files/image324.gif) ,
,
取學(xué)文科.files/image326.gif) 的中點
的中點學(xué)文科.files/image069.gif) , 連結(jié)
, 連結(jié)學(xué)文科.files/image329.gif) ,又
,又學(xué)文科.files/image331.gif) ,則
,則學(xué)文科.files/image333.gif) .
.
取學(xué)文科.files/image335.gif) 的中點
的中點學(xué)文科.files/image337.gif) ,連結(jié)
,連結(jié)學(xué)文科.files/image339.gif) ,則
,則學(xué)文科.files/image341.gif) ,
,學(xué)文科.files/image343.gif) .
.
學(xué)文科.files/image345.gif) 為二面角
為二面角學(xué)文科.files/image203.gif) 的平面角.
的平面角.
連結(jié)學(xué)文科.files/image348.gif) ,在
,在學(xué)文科.files/image350.gif) 中,
中,學(xué)文科.files/image352.gif) ,
,學(xué)文科.files/image354.gif) ,
,
取學(xué)文科.files/image356.gif) 的中點
的中點學(xué)文科.files/image358.gif) ,連結(jié)
,連結(jié)學(xué)文科.files/image360.gif) ,
,學(xué)文科.files/image362.gif) ,
,
在學(xué)文科.files/image364.gif) 中,
中,學(xué)文科.files/image366.gif) ,
,學(xué)文科.files/image368.gif) ,
,學(xué)文科.files/image370.gif) .
.
學(xué)文科.files/image372.gif) .
.
學(xué)文科.files/image374.gif) 二面角
二面角學(xué)文科.files/image203.gif) 的余弦值為
的余弦值為學(xué)文科.files/image377.gif) .
.
解法二:
(I)以學(xué)文科.files/image104.gif) 為原點,
為原點,學(xué)文科.files/image380.gif) 所在直線分別為
所在直線分別為學(xué)文科.files/image382.gif) 軸,
軸,學(xué)文科.files/image384.gif) 軸,
軸,學(xué)文科.files/image386.gif) 軸建立如圖所示的空間直角坐標(biāo)系,則
軸建立如圖所示的空間直角坐標(biāo)系,則學(xué)文科.files/image388.gif) ,
,學(xué)文科.files/image390.gif) ,
,學(xué)文科.files/image392.gif) ,
,學(xué)文科.files/image394.gif) ,
,學(xué)文科.files/image396.gif) ,
,學(xué)文科.files/image398.gif) .
.
學(xué)文科.files/image399.gif)
學(xué)文科.files/image401.gif) ,
,學(xué)文科.files/image403.gif) ,
,學(xué)文科.files/image405.gif)
學(xué)文科.files/image407.gif)
學(xué)文科.files/image409.gif)
又因為學(xué)文科.files/image315.gif) 所以,
所以,學(xué)文科.files/image199.gif) 平面
平面學(xué)文科.files/image201.gif) .
.
(II)設(shè)學(xué)文科.files/image411.gif) 為平面
為平面學(xué)文科.files/image413.gif) 的一個法向量.
的一個法向量.
由學(xué)文科.files/image415.gif) ,
,學(xué)文科.files/image417.gif) ,
,學(xué)文科.files/image419.gif)
學(xué)文科.files/image401.gif)
得學(xué)文科.files/image421.gif) 取
取學(xué)文科.files/image423.gif) ,則
,則學(xué)文科.files/image425.gif) .
.
又學(xué)文科.files/image427.gif) ,
,學(xué)文科.files/image401.gif) ,設(shè)
,設(shè)學(xué)文科.files/image430.gif) 為平面
為平面學(xué)文科.files/image432.gif) 的一個法向量,
的一個法向量,
由學(xué)文科.files/image434.gif) ,
,學(xué)文科.files/image436.gif) ,得
,得學(xué)文科.files/image438.gif) 取
取學(xué)文科.files/image440.gif) ,則
,則學(xué)文科.files/image442.gif) ,
,
設(shè)學(xué)文科.files/image444.gif) 與
與學(xué)文科.files/image446.gif) 的夾角為
的夾角為學(xué)文科.files/image448.gif) ,二面角
,二面角學(xué)文科.files/image203.gif) 為
為學(xué)文科.files/image451.gif) ,顯然
,顯然學(xué)文科.files/image451.gif) 為銳角,
為銳角,
學(xué)文科.files/image453.gif) ,
,
21.(本題滿分12分)
解:(Ⅰ) 學(xué)文科.files/image455.gif) ,
,學(xué)文科.files/image091.gif) 在
在學(xué)文科.files/image458.gif) 上是增函數(shù),在
上是增函數(shù),在學(xué)文科.files/image460.gif) 上是減函數(shù),
上是減函數(shù),
∴當(dāng)學(xué)文科.files/image462.gif) 時,
時, 學(xué)文科.files/image091.gif) 取得極大值.
取得極大值.
∴學(xué)文科.files/image464.gif) 即
即學(xué)文科.files/image158.gif) .
.
由學(xué)文科.files/image467.gif) ,
,學(xué)文科.files/image469.gif) 得
得學(xué)文科.files/image471.gif) ,
,
則有 學(xué)文科.files/image473.gif) ,
,學(xué)文科.files/image475.gif)
學(xué)文科.files/image382.gif)
學(xué)文科.files/image207.gif)
學(xué)文科.files/image479.gif)
學(xué)文科.files/image481.gif)
學(xué)文科.files/image483.gif)
學(xué)文科.files/image485.gif)
學(xué)文科.files/image487.gif)
學(xué)文科.files/image489.gif)
學(xué)文科.files/image479.gif)
學(xué)文科.files/image491.gif)
學(xué)文科.files/image479.gif)
學(xué)文科.files/image489.gif)
學(xué)文科.files/image091.gif)
遞增
極大值4
遞減
極小值0
遞增
所以, 當(dāng)學(xué)文科.files/image213.gif) 時,函數(shù)
時,函數(shù)學(xué)文科.files/image091.gif) 的極大值為4;極小值為0; 單調(diào)遞增區(qū)間為
的極大值為4;極小值為0; 單調(diào)遞增區(qū)間為學(xué)文科.files/image207.gif) 和
和學(xué)文科.files/image485.gif) .
.
(Ⅱ) 由(Ⅰ)知學(xué)文科.files/image158.gif) ,
, 學(xué)文科.files/image495.gif) ,
,學(xué)文科.files/image497.gif) 的兩個根分別為
的兩個根分別為學(xué)文科.files/image499.gif) . ∵
. ∵學(xué)文科.files/image091.gif) 在
在學(xué)文科.files/image460.gif) 上是減函數(shù),∴
上是減函數(shù),∴學(xué)文科.files/image502.gif) ,即
,即學(xué)文科.files/image504.gif) ,
,
學(xué)文科.files/image506.gif) .
.
22.(本題滿分12分)
解:(I)依題意,可知學(xué)文科.files/image508.gif) ,
,
∴ 學(xué)文科.files/image510.gif) ,解得
,解得學(xué)文科.files/image512.gif)
∴橢圓的方程為學(xué)文科.files/image514.gif)
(II)直線學(xué)文科.files/image231.gif) :
:學(xué)文科.files/image516.gif) 與⊙
與⊙學(xué)文科.files/image518.gif) 相切,則
相切,則學(xué)文科.files/image520.gif) ,即
,即學(xué)文科.files/image522.gif) ,
,
由學(xué)文科.files/image524.gif) ,得
,得學(xué)文科.files/image526.gif) ,
,
∵直線學(xué)文科.files/image231.gif) 與橢圓交于不同的兩點
與橢圓交于不同的兩點學(xué)文科.files/image235.gif) 設(shè)
設(shè)學(xué)文科.files/image528.gif)
∴學(xué)文科.files/image530.gif) ,
,
學(xué)文科.files/image532.gif)
學(xué)文科.files/image534.gif) ,
,
∴學(xué)文科.files/image536.gif)
∴學(xué)文科.files/image538.gif) ∴
∴學(xué)文科.files/image540.gif) ,
,
∴學(xué)文科.files/image542.gif)
學(xué)文科.files/image544.gif)
設(shè)學(xué)文科.files/image546.gif) ,則
,則學(xué)文科.files/image548.gif) ,
,學(xué)文科.files/image550.gif)
∵學(xué)文科.files/image552.gif) 在
在學(xué)文科.files/image554.gif) 上單調(diào)遞增
∴
上單調(diào)遞增
∴學(xué)文科.files/image556.gif) .
.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com