
題目列表(包括答案和解析)
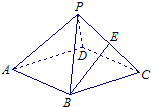 在棱長均為2的正四棱錐P-ABCD中,點E為PC的中點,則下列命題正確的是( )
在棱長均為2的正四棱錐P-ABCD中,點E為PC的中點,則下列命題正確的是( )A、BE∥平面PAD,且BE到平面PAD的距離為
| ||||
B、BE∥平面PAD,且BE到平面PAD的距離為
| ||||
| C、BE與平面PAD不平行,且BE與平面PAD所成的角大于30° | ||||
| D、BE與平面PAD不平行,且BE與平面PAD所成的角小于30° |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
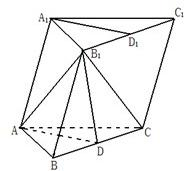 如圖,在棱長均為4的三棱柱ABC-A1B1C1中,D、D1分別是BC和B1C1的中點.
如圖,在棱長均為4的三棱柱ABC-A1B1C1中,D、D1分別是BC和B1C1的中點. (2010•泰安一模)如圖,在棱長均為1的三棱錐S-ABC中,E為棱SA的中點,F為△ABC的中心,則直線EF與平面ABC所成角的正切值是( )
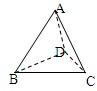
(2010•泰安一模)如圖,在棱長均為1的三棱錐S-ABC中,E為棱SA的中點,F為△ABC的中心,則直線EF與平面ABC所成角的正切值是( ) 如圖,在棱長均為a的三棱錐A-BCD中,E為BC的中點,求異面直線AE和BD所成角的余弦值.
如圖,在棱長均為a的三棱錐A-BCD中,E為BC的中點,求異面直線AE和BD所成角的余弦值.一、選擇題(本大題共8小題,每小題5分,共40分)
ACDDB CDC
二、填空題(本大題共6小題,每小題5分.有兩空的小題,第一空3分,第二空2分,共30分)
(9)62 (10)2 (11).files/image254.gif) (12)2,
(12)2,.files/image256.gif)
(13).files/image258.gif) (14)
(14).files/image260.gif) ,③④
,③④
三、解答題(本大題共6小題,共80分)
(15)(本小題共13分)
解:(Ⅰ)∵.files/image150.gif) (
(.files/image154.gif) ),
),
∴.files/image262.gif) (
(.files/image154.gif) ).
………………………1分
).
………………………1分
∵.files/image156.gif) ,
,.files/image158.gif) ,
,.files/image160.gif) 成等差數列,
成等差數列,
∴.files/image264.gif) .
…………………………3分
.
…………………………3分
∴.files/image266.gif) .
………………………………………5分
.
………………………………………5分
∴.files/image268.gif) .
………………………………………6分
.
………………………………………6分
(Ⅱ)由(Ⅰ)得
.files/image270.gif) (
(.files/image154.gif) ).
).
∴數列.files/image272.gif) 為首項是
為首項是.files/image274.gif) ,公差為1的等差數列. ………………………8分
,公差為1的等差數列. ………………………8分
∴.files/image276.gif) .
.
∴.files/image278.gif) .
……………………………………10分
.
……………………………………10分
當.files/image280.gif) 時,
時,.files/image282.gif) . ………………………12分
. ………………………12分
當.files/image284.gif) 時,上式也成立.
……………………13分
時,上式也成立.
……………………13分
∴.files/image286.gif) (
(.files/image154.gif) ).
).
(16)(本小題共13分)
解:(Ⅰ)該間教室兩次檢測中,空氣質量均為A級的概率為.files/image288.gif) .……………2分
.……………2分
該間教室兩次檢測中,空氣質量一次為A級,另一次為B級的概率為.files/image290.gif) .
.
…………………………4分
設“該間教室的空氣質量合格”為事件E.則 …………………………………5分
.files/image292.gif) .
…………………………………6分
.
…………………………………6分
答:估計該間教室的空氣質量合格的概率為.files/image294.gif) .
.
(Ⅱ)由題意可知,.files/image166.gif) 的取值為0,1,2,3,4.
………………7分
的取值為0,1,2,3,4.
………………7分
.files/image296.gif)
.files/image298.gif) .
.
隨機變量.files/image166.gif) 的分布列為:
的分布列為:
.files/image166.gif)
0
1
2
3
4
.files/image211.gif)
.files/image302.gif)
.files/image304.gif)
.files/image306.gif)
.files/image308.gif)
.files/image310.gif)
……………………………12分
解法一:
∴.files/image312.gif) . ………………13分
. ………………13分
解法二:.files/image314.gif)
.files/image316.gif) ,
,
∴.files/image318.gif) .
………………13分
.
………………13分
(17)(本小題共14分)
(Ⅰ)證明:設.files/image178.gif) 的中點為
的中點為.files/image077.gif) .
.
在斜三棱柱.files/image170.gif) 中,點
中,點.files/image174.gif) 在底面
在底面.files/image176.gif) 上的射影恰好是
上的射影恰好是.files/image178.gif) 的中點,
的中點,
.files/image314.gif)
.files/image326.gif) 平面
平面.files/image176.gif) ,
,
.files/image328.gif) .
……………………2分
.
……………………2分
.files/image314.gif)
.files/image172.gif) ,
,
∴.files/image331.gif) .
.
.files/image314.gif)
.files/image333.gif) ,
,
∴.files/image335.gif) 平面
平面.files/image184.gif) . ……………………4分
. ……………………4分
.files/image314.gif)
.files/image337.gif) 平面
平面.files/image339.gif) ,
,
.files/image341.gif) 平面
平面.files/image182.gif) 平面
平面.files/image184.gif) . …………………………5分
. …………………………5分
解法一:(Ⅱ)連接.files/image343.gif) ,
,.files/image314.gif)
.files/image335.gif) 平面
平面.files/image184.gif) ,
,
.files/image346.gif) 是直線
是直線.files/image348.gif) 在平面
在平面.files/image184.gif) 上的射影. …………………………5分
上的射影. …………………………5分
.files/image314.gif)
.files/image351.gif) ,
,
.files/image341.gif) 平行四邊形
平行四邊形.files/image184.gif) 是菱形.
是菱形.
.files/image355.gif) .
………………………………………7分
.
………………………………………7分
.files/image357.gif) .
……………………………………9分
.
……………………………………9分
.files/image369.gif) ,
,.files/image371.gif)
.files/image373.gif) 平面
平面.files/image375.gif) .
.
.files/image377.gif) .
.
.files/image379.gif) 是二面角
是二面角.files/image190.gif) 的平面角.
………………………………………11分
的平面角.
………………………………………11分
設.files/image381.gif) ,則
,則.files/image383.gif)
.files/image314.gif)
.files/image385.gif) ,
,
.files/image387.gif) .
.
.files/image389.gif) .
.
.files/image391.gif)
.files/image393.gif) .
.
.files/image395.gif) .
.
.files/image397.gif) 平面
平面.files/image186.gif) ,
,.files/image400.gif) 平面
平面.files/image186.gif) ,
,
.files/image402.gif) .
.
.files/image404.gif) .
.
在.files/image406.gif) 中,可求
中,可求.files/image408.gif) .
.
∵.files/image410.gif) ,∴
,∴.files/image412.gif) .
.
∴.files/image414.gif) .
.
.files/image416.gif) .
……………………………………13分
.
……………………………………13分
.files/image418.gif) .
.
∴二面角.files/image190.gif) 的大小為
的大小為.files/image420.gif) . …………………………14分
. …………………………14分
.files/image422.gif) 解法二:(Ⅱ)因為點
解法二:(Ⅱ)因為點.files/image174.gif) 在底面
在底面.files/image176.gif) 上的射影是
上的射影是.files/image178.gif) 的中點,設
的中點,設.files/image178.gif) 的中點為
的中點為.files/image427.gif) ,則
,則.files/image429.gif) 垂直平面ABC.以
垂直平面ABC.以.files/image427.gif) 為原點,過
為原點,過.files/image427.gif) 平行于
平行于.files/image431.gif) 的直線為
的直線為.files/image217.gif) 軸,
軸,.files/image178.gif) 所在直線為
所在直線為.files/image434.gif) 軸,
軸,.files/image436.gif) 所在直線為
所在直線為.files/image438.gif) 軸,建立如圖所示的空間直角坐標系.
軸,建立如圖所示的空間直角坐標系.
設.files/image440.gif) ,由題意可知,
,由題意可知,.files/image442.gif) .
.
設.files/image444.gif) ,由
,由.files/image446.gif) ,得
,得.files/image448.gif) ……………………………7分
……………………………7分
.files/image450.gif) .
.
又.files/image452.gif) .
.
.files/image454.gif) .
.
.files/image357.gif) .
………………………………………9分
.
………………………………………9分
(Ⅲ)設平面.files/image457.gif) 的法向量為
的法向量為.files/image459.gif) .
.
則.files/image461.gif)
∴.files/image463.gif)
.files/image465.gif) .
.
設平面.files/image467.gif) 的法向量為
的法向量為.files/image469.gif) .則
.則.files/image471.gif)
∴.files/image473.gif)
.files/image475.gif) .
……………………………………12分
.
……………………………………12分
.files/image477.gif) .
…………………………………13分
.
…………………………………13分
.files/image341.gif) 二面角
二面角.files/image190.gif) 的大小為
的大小為.files/image420.gif) .
………………………………………14分
.
………………………………………14分
(18)(本小題共13分)
解:(Ⅰ)函數.files/image138.gif) 的定義域為
的定義域為.files/image481.gif) . ………………………………1分
. ………………………………1分
.files/image483.gif) . …………………………3分
. …………………………3分
由.files/image485.gif) ,解得
,解得.files/image487.gif) .
.
由.files/image489.gif) ,解得
,解得.files/image491.gif) 且
且.files/image493.gif) .
.
∴.files/image138.gif) 的單調遞增區間為
的單調遞增區間為.files/image496.gif) ,單調遞減區間為
,單調遞減區間為.files/image498.gif) ,
,.files/image500.gif) .
.
………………………………………6分
(Ⅱ)由題意可知,.files/image502.gif) ,且
,且.files/image192.gif) 在
在.files/image504.gif) 上的最小值小于等于
上的最小值小于等于.files/image260.gif) 時,存在實數
時,存在實數.files/image197.gif) ,使得不等式
,使得不等式.files/image199.gif) 成立.
………………………………………7分
成立.
………………………………………7分
若.files/image507.gif) 即
即.files/image509.gif) 時,
時,
x
.files/image500.gif)
a+1
.files/image512.gif)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com