題目列表(包括答案和解析)
對于函數
，如果存在實數
使得
，那么稱
為
的生成函數．
（1）下面給出兩組函數，是否分別為的生成函數？并說明理由；
第一組：
；
第二組：
；
（2）設
，生成函數．若不等式
在
上有解，求實數
的取值范圍；
（3）設
，取
，生成函數圖像的最低點坐標為
．若對于任意正實數
且
．試問是否存在最大的常數
，使
恒成立？如果存在，求出這個的值；如果不存在，請說明理由．
對于函數
，如果存在實數
使得
，那么稱
為
的生成函數．
（1）下面給出兩組函數，是否分別為的生成函數？并說明理由；
第一組：
；
第二組：
；
（2）設
，生成函數．若不等式
在
上有解，求實數
的取值范圍；
（3）設
，取
，生成函數使
恒成立，求
的取值范圍．
設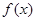
是定義在
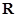上的增函數，且對于任意的都有
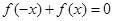恒成立. 如果實數
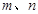滿足不等式
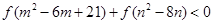,那么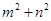
的取值范圍是
A. (9, 49) B. (13, 49) C.(9, 25) D. (3, 7)
設
是定義在
上的增函數，且對于任意的
都有
恒成立． 如果實數
滿足不等式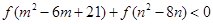
,xxk那么
的取值范圍是 
設
是定義在
上的增函數，且對于任意的
都有
恒成立.如果實數
滿足不等式
,那么
的取值范圍是
一、
1．B 2．A 3．D 4．A 5．C 6．A 7．D 8．B 9．D 10．A
11．A 12．B
1．由題意知
，解得
．
2．由
得
，化得
，解得
．
3．
，又
．
4．設
到
的角為
的斜率
的斜率
，
則
，于是
．
5．由條件，解
即
得
，則
．
6．不等式組化得 
平面區域如圖所示，陰影部分面積：
．
7．由已知得
，而
，則
是以3為公比的等比數列．
8．
即
，于是
，而
解得
．
9．函數可化為
，令
，
可得其對稱中心為
，當
時得對稱中心為
．
10．
．
11．由條件得：
，則
得
所以
．
12．沿球面距離運動路程最短，最短路程可以選
．
二、填空題
13．
，由
與
垂直得
．即
，解得
14．99
在等差數列
中，
也是等差數列，由等差中項定理得
．
所以
．
15．
由題意知，直線
是拋物線
的準線，而
到的距離等于到焦點
的距離．即求點到點
的距離與到點
的距離和的最小值，就是點與點的距離，為．
16．②
一方面．由條件，
，得
，故②正確．
另一方面，如圖，在正方體
中，把
、
分別記作、
，平面
、平面
、平面
分別記作
、
、
，就可以否定①與③．
三、解答題
17．解：
，且
，即
又
．
由余弦定理，
，故
．
18．解：（1）只有甲解出的概率：
．
（2）只有1人解出的概率：
．
19．解：（1）由已知
，∴數列
的公比
，首項
又數列
中，
∴數列的公差
，首項
∴數列、
的通項公式依次為
．
（2）
，
．
20．（1）證明；在直三棱柱
中，
面
又
面
，而
面
，
∴平面
平面
（2）解：取
中點
，連接
交
于點，則
．
與平面所成角大小等于與平面所成角的大小．
取
中點
，連接
、
，則等腰三角形
中，
．
又由（1）得
面
．
面
為直線與面所成的角
又
，
∴直線與平面所成角的正切值為
．
（注：本題也可以能過建立空間直角坐標系解答）
21．解：（1）設橢圓方程為
，雙曲線方程為
，半焦距
由已知得
，解得
，則
故橢圓及雙曲線方程分別為
及
．
（2）向量
與
的夾解即是
，設
，則
由余弦定理得
①
由橢圓定義得
②
由雙曲線定義得
③
式②+式③得
，式②
式③得
將它們代入式①得
，解得
，所以向量與夾角的余弦值為
．
22．解（1）由
得
在
處有極值
①
又
在
處的切線的傾斜角為
②
由式①、式②解得
設的方程為
∵原點
到直線的距離為
，
解得
．
又不過第四象限，
．
所以切線的方程為
．
切點坐標為（2，3），則
，
解得
．
（2）
在
上遞增，在
上遞減
而
在區間
上的最大值是3，最小值是
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com