
題目列表(包括答案和解析)
C.選修4—4:坐標系與參數(shù)方程
(本小題滿分10分)
在極坐標系中,圓 的方程為
的方程為 ,以極點為坐標原點,極軸為
,以極點為坐標原點,極軸為 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),判斷直線
為參數(shù)),判斷直線 和圓
和圓 的位置關系.
的位置關系.
C.選修4-4:坐標系與參數(shù)方程(本小題滿分10分)
在平面直角坐標系 中,求過橢圓
中,求過橢圓 (
( 為參數(shù))的右焦點且與直線
為參數(shù))的右焦點且與直線 (
( 為參數(shù))平行的直線的普通方程。
為參數(shù))平行的直線的普通方程。
C.(選修4—4:坐標系與參數(shù)方程)
在極坐標系中,圓 的方程為
的方程為 ,以極點為坐標原點,極軸為
,以極點為坐標原點,極軸為 軸的正
軸的正
半軸建立平面直角坐標系,直線 的參數(shù)方程為
的參數(shù)方程為 (
( 為參數(shù)),求直線
為參數(shù)),求直線 被
被 截
截
得的弦 的長度.
的長度.
C.(坐標系與參數(shù)方程選做題)已知極坐標的極點在直角坐標系的原點O處,極軸與x軸的正半軸重合,曲線C的參數(shù)方程為 (
( 為參數(shù)),直線l的極坐標方程為
為參數(shù)),直線l的極坐標方程為 .點P在曲線C上,則點P到直線l的距離的最小值為
.
.點P在曲線C上,則點P到直線l的距離的最小值為
.
C.選修4-4:坐標系與參數(shù)方程
在直角坐標系 中,已知曲線
中,已知曲線 的參數(shù)方程是
的參數(shù)方程是 (
( 是參數(shù)),若以
是參數(shù)),若以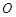 為極點,
為極點, 軸的正半軸為極軸,取與直角坐標系中相同的單位長度,建立極坐標系,求曲線
軸的正半軸為極軸,取與直角坐標系中相同的單位長度,建立極坐標系,求曲線 的極坐標方程.
的極坐標方程.
一、選擇題:本答題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的,把它選出來填涂在答題卡上。
1.A
2.D 對“若 則
則 ”的否定已經(jīng)不是“四種命題”中的任何一種,而是表示“合取”命題;
”的否定已經(jīng)不是“四種命題”中的任何一種,而是表示“合取”命題; 且非
且非 ,即反設命題的結論不成立為非
,即反設命題的結論不成立為非 ,選D。
,選D。
3.B 因為 ,所以,當
,所以,當 時,分母
時,分母 最小,從而
最小,從而 最大為2,選B。
最大為2,選B。
4.C
5.B 設等差數(shù)列 的前三項為
的前三項為 (其中
(其中 ),則
),則
 于是它的首項是2,選B
于是它的首項是2,選B
6.D 因為 的反函數(shù)的圖像經(jīng)過點
的反函數(shù)的圖像經(jīng)過點 ,所以函數(shù)
,所以函數(shù) 的圖像經(jīng)過點
的圖像經(jīng)過點 ,于是
,于是 ,解得
,解得 ,選D
,選D
7.D 在直角坐標系中較準確地作出點A、B、C,并結合代值驗證,可知A、C兩點的坐標不滿足選擇支D的解析式,選D。
8.C 因為 是定義在R上的奇函數(shù),所以
是定義在R上的奇函數(shù),所以 ,又
,又 ,故函數(shù)
,故函數(shù) 的周期為4,所以
的周期為4,所以 ,選C
,選C
9.A 函數(shù)的定義域為(0,+ ),當
),當 ≥1時,
≥1時, ≥0,有
≥0,有 ;當
;當 時,
時, ,有
,有 ,選A。
,選A。
10.B 根據(jù)圖像可知,當 時,函數(shù)圖像從左到右是上升的,表明對數(shù)函數(shù)是增函數(shù),∴a、b均大于1,排除C、D。于是取
時,函數(shù)圖像從左到右是上升的,表明對數(shù)函數(shù)是增函數(shù),∴a、b均大于1,排除C、D。于是取 =2,得
=2,得 ,有
,有

 ,選B.
,選B.
11.A
12.C 設 ,則B
,則B ,有
,有

 ,∴
,∴ 。由于A、B兩點在函數(shù)
。由于A、B兩點在函數(shù) 的圖象上,則
的圖象上,則 =1,∴
=1,∴ ,而點A又在函數(shù)
,而點A又在函數(shù) 的圖像上,∴
的圖像上,∴ ,得
,得 ,有
,有 ,于是
,于是 ,選C。
,選C。
13.
14.原式=
15.由圖知車速小于
16.(1)當 時,
時,
(2)當 時,
時,
(3)當 時,
時,
所以,在區(qū)間 上,當
上,當 時函數(shù)
時函數(shù) 取得最小值
取得最小值
三、解答題:本答題共6小題,共74分,解答應寫出文字說明、證明過程或驗算步驟。
17.(本題滿分12分)
解法一 原不等式等價于
 或
或
………………12分
解法二 原不等式等價于
 或
或
 或
或
說明 本題是教材第一冊上 頁習題1.5第5題:解不等式
頁習題1.5第5題:解不等式 的改變,這是關于
的改變,這是關于 的二次雙連不等式,若轉(zhuǎn)化為兩個二次不等式組成的不等式組來解時,只要善于正確因式分解,數(shù)軸標根,也能快速解決。
的二次雙連不等式,若轉(zhuǎn)化為兩個二次不等式組成的不等式組來解時,只要善于正確因式分解,數(shù)軸標根,也能快速解決。
18.∵ ,∴
,∴ 是奇函數(shù)。
是奇函數(shù)。
∵ ,當
,當 時,
時, 是減函數(shù),
是減函數(shù),
∴ 在(-1,1)內(nèi)是減函數(shù).
…………8分
在(-1,1)內(nèi)是減函數(shù).
…………8分
 .
.
故編號為①③的結論正確,編號為②的結論不正確 ……12分
事實上,還有∵ ,∴
,∴ 。
。
本題是教材85頁4題、99頁例3、101頁6、7題102頁1題的綜合與改編。
19.(本題滿分12分)
設 表示每臺的利潤,y表示周銷售量,則
表示每臺的利潤,y表示周銷售量,則 經(jīng)過了點(20,0),(0,35),
經(jīng)過了點(20,0),(0,35),
∴ 解得
解得 ………………4分
………………4分
即 或
或 ,其中
,其中
因此,商店一周中所獲利潤總額為:
每臺利潤×銷售量=
= ………8分
………8分
由于y是正整數(shù),所以當周銷售量為y=17或18時,利潤總額最大,為 元,此時
元,此時 元或10.3元。
………………12分
元或10.3元。
………………12分
20.甲種水稻的平均畝產(chǎn)量為 甲=
甲=
乙種水稻的平均畝產(chǎn)量為 乙=
乙=
表明兩種水稻的平均畝產(chǎn)量相等。 ……………6分
其方差為 =
=
 =
=
 即有
即有 >
> ,這說明乙種水稻其畝產(chǎn)量較為穩(wěn)定……12分
,這說明乙種水稻其畝產(chǎn)量較為穩(wěn)定……12分
21.(本題滿分12分)
(1)延長FE與AB交于點P,則
∵EP//BC,∴ ∽
∽ ,
,
∴ ,即
,即 ,∴
,∴ ,
…………2分
,
…………2分
在直角三角形AEP中, ,
, ,
, ,
,
由勾股定理,得 (*)
(*)
即 。
………………6分
。
………………6分
∵ ∴(*)式成立的充要條件是
∴(*)式成立的充要條件是 ,
,
所以y與x的函數(shù)關系式為 , ……8分
, ……8分
(2)因為 ,等號當且僅當
,等號當且僅當 ,即
,即 時取得,
………10分
時取得,
………10分
所以正方形 的面積
的面積 當
當 時取得最大值
時取得最大值 ………12分
………12分
若由 得
得 ,
,
所以 即
即 ,
,
等式右端分子有理化,得
∴ ∵
∵ ∴
∴ ,
,
整理,得 與
與 的函數(shù)關系式為
的函數(shù)關系式為 (
( )
)
22. 。
………………2分
。
………………2分
若 ,則
,則 ,知
,知 單調(diào)遞減,而
單調(diào)遞減,而 ,∴
,∴
若 ,令
,令 ,則
,則 。
。
∵ ,則只需考慮
,則只需考慮 的情況:
的情況:
(1)當 ,即
,即 時,
時,
若 時,
時, ,則
,則
若 時,
時, ,則
,則
∴ 極大值=
極大值= 。
…9分
。
…9分
(2)當 即
即 時,∵
時,∵ ,∴
,∴ ,
,
故 ,知
,知 是增函數(shù),∴
是增函數(shù),∴ ……12分
……12分
綜上所述,當 時,
時, 的最大值為0;當
的最大值為0;當 ,
, 時,
時, 的最大值為
的最大值為 ;當
;當 時,
時, 的最大值為
的最大值為 ……14分
……14分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com