
題目列表(包括答案和解析)
| x(年) | 3 | 4 | 5 | 6 |
| y(萬元) | 2.5 | 3 | 4 | 4.5 |
| ? |
| y |
下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量![]() (噸)與相應的生產能耗
(噸)與相應的生產能耗![]() (噸標準煤)的幾組對照數據
(噸標準煤)的幾組對照數據
|
|
|
|
|
|
|
|
|
|
|
|
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)已知該廠技改前100噸甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性
回歸方程,預測生產100噸甲產品的生產能耗比技改前降低多少噸標準煤?
下表提供了某廠節能降耗技術發行后,生產甲產品過程中記錄的產量 (噸)與相應的生產能耗y(噸標準煤)的幾組對應數據.
(噸)與相應的生產能耗y(噸標準煤)的幾組對應數據.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 所表示的直線必經過的點;
所表示的直線必經過的點; ;
; )
)下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(t)與相應的生產能耗y(t標準煤)的幾組對照數據.
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程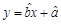 ;
;
(3)已知該廠技術改造前100t甲產品的生產能耗為90t標準煤,試根據(2)求出的線性回歸方程預測生產100t甲產品的生產能耗比技術改造前降低多少噸標準煤?
下表提供了某廠節能降耗技術改革后生產甲產品過程中記錄的產量x(t)與相應的生產能耗Y(噸標準煤)的幾組對照數據:
|
x |
3 |
4 |
5 |
6 |
|
y |
2.5 |
3 |
4 |
4.5 |
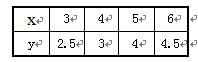
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程;
(3)已知該廠技改前生產100 t甲產品的生產能耗為90噸標準煤.試根據(2)求出的線性回歸方程,預測生產100 t甲產品的生產能耗比技改前降低多少噸標準煤?
(參考數值:3×2.5 + 4×3 + 5×4 + 6×4.5=66.5)
一、填空題
1、 2、
2、 3、(1)(2)(3)(4) 4、
3、(1)(2)(3)(4) 4、 5、
5、 6、3
6、3
7、 8、
8、 9、
9、 10、不能 11、
10、不能 11、 12、46 13、
12、46 13、
14、(3)(4)
二、解答題
15、解:(1)sin3α=sin(2α+α)=sin2αcosα+cos2αsinα
=2sinαcos2α+(1-2sin2α)sinα
=2sinα(1-sin2α)+(1-2sin2α)sinα=3sinα-4sin3α .
(2)∵sin54°=cos36°,
∴3sin18°-4sin318°=1-2sin18°.
令t= sin18°,則上式可變形為3t-4t3=1-2t2,即
(t-1)(4t2+2t-1)=0.
解得  (t= 1與
(t= 1與 均不合,舍去).
均不合,舍去).
∴sin18°= .
.
16、證明:(1)連結 ,在
,在 中,
中, 、
、 分別為
分別為 ,
, 的中點,則
的中點,則


(2)





3)
 且
且 
 ,
,

∴ 即
即
 =
=
=
17、解:由已知圓的方程為 ,
,
按 平移得到
平移得到 .
.
∵ ∴
∴ .
.
即 .
.
又 ,且
,且 ,∴
,∴ .∴
.∴ .
.
設 ,
,
 的中點為D.
的中點為D.
由 ,則
,則 ,又
,又 .
.
∴ 到
到 的距離等于
的距離等于 .
.
即 , ∴
, ∴ .
.
∴直線 的方程為:
的方程為: 或
或 .
.
18、解:(1)如下圖

(2) =3
=3 2.5+4
2.5+4 3+5
3+5 4+6
4+6 4.5=66.5
4.5=66.5
 =
= =4.5
=4.5
 =
= =3.5
=3.5



故線性回歸方程為y=0.7x+0.35
(3)根據回歸方程的預測,現在生產100噸產品消耗的標準煤的數量為0.7 100+0.35=70.35
100+0.35=70.35
故耗能減少了90-70.35=19.65(噸)
19、解:(1)由
 是首項為
是首項為 ,公比為
,公比為 的等比數列
的等比數列
當 時,
時, ,
,
所以

(2)由 得
得
 (作差證明)
(作差證明)

綜上所述當 時,不等式
時,不等式 對任意
對任意 都成立.
都成立.
20.解:(1) ,由題意及導數的幾何意義得
,由題意及導數的幾何意義得
 ,
, (1)
(1)
 ,
(2)
,
(2)
又 ,可得
,可得 ,即
,即 ,故
,故
由(1)得 ,代入
,代入 ,再由
,再由 ,得
,得
 ,
(3)
,
(3)
將 代入(2)得
代入(2)得 ,即方程
,即方程 有實根.
有實根.
故其判別式 得
得
 ,或
,或 ,
(4)
,
(4)
由(3),(4)得 ;
;
(2)由 的判別式
的判別式 ,
,
知方程 有兩個不等實根,設為
有兩個不等實根,設為 ,
,
又由 知,
知, 為方程(
為方程( )的一個實根,則有根與系數的關系得
)的一個實根,則有根與系數的關系得
 ,
,
當 或
或 時,
時, ,當
,當 時,
時, ,
,
故函數 的遞增區間為
的遞增區間為 ,由題設知
,由題設知 ,
,
因此 ,由(Ⅰ)知
,由(Ⅰ)知 得
得
 的取值范圍為
的取值范圍為 ;
;
(3)由 ,即
,即 ,即
,即 ,
,
因為 ,則
,則 ,整理得
,整理得 ,
,
設 ,可以看作是關于
,可以看作是關于 的一次函數,
的一次函數,
由題意 對于
對于 恒成立,
恒成立,
故 即
即 得
得 或
或 ,
,
由題意, ,
,
故 ,因此
,因此 的最小值為
的最小值為 .
.
理科加試題:
1、(1)“油罐被引爆”的事件為事件A,其對立事件為 ,則P(
,則P( )=C
)=C
∴P(A)=1- 答:油罐被引爆的概率為
答:油罐被引爆的概率為
(2)射擊次數ξ的可能取值為2,3,4,5,
P(ξ=2)= , P(ξ=3)=C
, P(ξ=3)=C ,
,
P(ξ=4)=C , P(ξ=5)=C
, P(ξ=5)=C
ξ
2
3
4
5




故ξ的分布列為:
Eξ=2× +3×
+3× +4×
+4× +5×
+5× =
=
2、解:(1)由圖形可知二次函數的圖象過點(0,0),(8,0),并且f(x)的最大值為16
則 ,
,
∴函數f(x)的解析式為
(2)由 得
得
∵0≤t≤2,∴直線l1與f(x)的圖象的交點坐標為(
由定積分的幾何意義知:



選做
1、解:(1)證明:連結 .
.
因為 與圓
與圓 相切于點
相切于點 ,所以
,所以 .
.
因為 是圓
是圓 的弦
的弦 的中點,所以
的中點,所以 .
.
于是 .
.
由圓心 在
在 的內部,可知四邊形
的內部,可知四邊形 的對角互補,所以
的對角互補,所以 四點共圓.
四點共圓.
(2)解:由(Ⅰ)得 四點共圓,所以
四點共圓,所以 .
.
由(Ⅰ)得 .
.
由圓心 在
在 的內部,可知
的內部,可知 .
.
所以 .
.
2、解:在矩陣N=
 的作用下,一個圖形變換為其繞原點逆時針旋轉
的作用下,一個圖形變換為其繞原點逆時針旋轉 得到的圖形,在矩陣M=
得到的圖形,在矩陣M=
 的作用下,一個圖形變換為與之關于直線
的作用下,一個圖形變換為與之關于直線 對稱的圖形。因此
對稱的圖形。因此
△ABC在矩陣MN作用下變換所得到的圖形與△ABC全等,從而其面積即為1
3、解:以極點為原點,極軸為 軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.
軸正半軸,建立平面直角坐標系,兩坐標系中取相同的長度單位.
(1) ,
, ,由
,由 得
得 .
.
所以 .
.
即 為
為 的直角坐標方程.
的直角坐標方程.
同理 為
為 的直角坐標方程.
的直角坐標方程.
(2)由
 解得
解得
 .
.
即 ,
, 交于點
交于點 和
和 .過交點的直線的直角坐標方程為
.過交點的直線的直角坐標方程為 .
.
 4、解:
4、解:
(1)令 ,則
,則
 ...............3分
...............3分
作出函數 的圖象,它與直線
的圖象,它與直線 的交點為
的交點為 和
和 .
.
所以 的解集為
的解集為 .
.
(2)由函數 的圖像可知,當
的圖像可知,當 時,
時, 取得最小值
取得最小值 .
.
等于△ABC的面積,
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com