
題目列表(包括答案和解析)
(14分)已知![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,右焦點
的左、右焦點,右焦點![]() 到上頂點的距離為2,若
到上頂點的距離為2,若![]()
(1)求此橢圓的方程;
(2)點![]() 是橢圓的右頂點,直線
是橢圓的右頂點,直線![]() 與橢圓交于
與橢圓交于![]() 、
、![]() 兩點(
兩點(![]() 在第一象限內),又
在第一象限內),又![]() 、
、![]() 是此橢圓上兩點,并且滿足
是此橢圓上兩點,并且滿足 ,求證:向量
,求證:向量![]() 與
與![]() 共線
共線
已知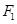 、
、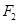 分別是橢圓
分別是橢圓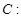
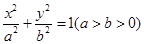 的左、右焦點,右焦點
的左、右焦點,右焦點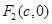 到上頂點的距離為2,若
到上頂點的距離為2,若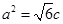
(Ⅰ)求此橢圓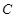 的方程;
的方程;
(Ⅱ)直線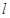 與橢圓
與橢圓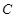 交于
交于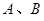 兩點,若弦
兩點,若弦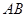 的中點為
的中點為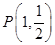 ,求直線
,求直線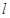 的方程.
的方程.
(12分)已知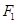 、
、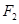 分別是橢圓
分別是橢圓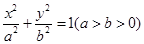 的左、右焦點,點B是其上頂點,橢圓的右準線與
的左、右焦點,點B是其上頂點,橢圓的右準線與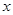 軸交于點N,且
軸交于點N,且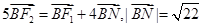 。
。
(1)求橢圓方程;
(2)直線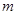 :
: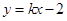 與橢圓交于不同的兩點M、Q,若△BMQ是以MQ為底邊的等腰三角形,求
與橢圓交于不同的兩點M、Q,若△BMQ是以MQ為底邊的等腰三角形,求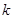 的值。
的值。
已知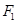 、
、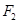 分別是橢圓
分別是橢圓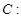
 的左、右焦點,右焦點
的左、右焦點,右焦點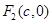 到上頂點的距離為2,若
到上頂點的距離為2,若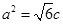
(Ⅰ)求此橢圓 的方程;
的方程;
(Ⅱ)直線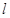 與橢圓
與橢圓 交于
交于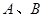 兩點,若弦
兩點,若弦 的中點為
的中點為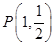 ,求直線
,求直線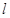 的方程.
的方程.
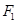 、
、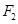 分別是橢圓
分別是橢圓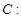
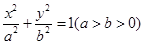 的左、右焦點,右焦點
的左、右焦點,右焦點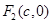 到上頂點的距離為2,若
到上頂點的距離為2,若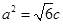
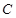 的方程;
的方程;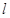 與橢圓
與橢圓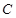 交于
交于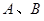 兩點,若弦
兩點,若弦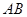 的中點為
的中點為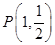 ,求直線
,求直線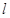 的方程.
的方程.一、選擇題:本大題共10小題,每小題5分,共50分。在每小題給出的四個選項中,只有一項是符合題目要求的。
題號
1
2
3
4
5
6
7
8
9
10
答案
D
B
A
A
C
B
C
B
C
D
二、填空題:(每小題4分,共24分)
11. 12.800,20% 13.2 14.4 15.
12.800,20% 13.2 14.4 15. 16.1005
16.1005
三、解答題:(17~20題,每小題12分,第21、22題14分,共計76分)
17.(本題滿分12分)
解:(1)在 中,利用余弦定理,
中,利用余弦定理, ,
,
代入 得,
得,
而 是銳角三角形,所以角
是銳角三角形,所以角 ??????????????????????? 5分
??????????????????????? 5分
(2)
周期
因為
所以 ????????????????????????? 8分
????????????????????????? 8分
當 時,
時, 又
又 ;
;
所以, 在
在 上的單調減區間為
上的單調減區間為 ???????? 12分
???????? 12分
18.(本題滿分12分)
解(I)設 為
為 的中點,連結
的中點,連結 ,
,
 為
為 的中點,
的中點, 為
為 的中點,
的中點,
 ==
==  ==
==
 ==
==

 ????????????????????????????????????????????????? 4分
????????????????????????????????????????????????? 4分
 (Ⅱ)
(Ⅱ)


(Ⅲ)由(Ⅱ)知 ,
,

19.(本題滿分12分)
解:(1)共有10個等可能性的基本事件,列舉如下:(1,2),(1,3),(1,4),(1,5),
(2,3),(2,4),(2,5)(3,4),(3,5),(4,5)。
(2)記事件“甲同學所抽取的兩題的編號之和小于8但不小于4”為事件A
由(1)可知事件共含有7個基本事件,列舉如下:(1,3),(1,4),(1,5),(2,3),
(2,4),(2,5),(3,4)
(3)記事件B“做對政治附加題同時還需做對兩道基本題”
記事件C“做對歷史附加題同時還需至少做對一道基本題”
記事件D“甲同學得分不低于20分”

20.(本題滿分12分)
(1)與由
切線的斜率 切點坐標
切點坐標
所求切線方程 ?????????????????????????????? 5分
?????????????????????????????? 5分
(2)若函數為 上單調增函數,
上單調增函數,
則 上恒成立,即不等式
上恒成立,即不等式 在
在 上恒成立。
上恒成立。
也即 在
在 上恒成立
上恒成立
令 ,上述問題等價于
,上述問題等價于
而 為在
為在 上的減函數,
上的減函數,
則 ,于是
,于是 為所求????????????????????????? 12分
為所求????????????????????????? 12分
21.(本題滿分14分)
解(1)由


(2)數列 為等差數列,公差
為等差數列,公差
從而

從而
22.(本題滿分14分)
解:(1)由題知: ????? 4分
????? 4分
(2)因為: ,從而
,從而 與
與 的平分線平行,
的平分線平行,
所以 的平分線垂直于
的平分線垂直于 軸;
軸;
由
不妨設 的斜率為
的斜率為 ,則
,則 的斜率
的斜率 ;因此
;因此 和
和 的方程分別為:
的方程分別為:
 、
、 ;其中
;其中 ;?????????? 8分
;?????????? 8分
由 得;
得;
因為 在橢圓上;所以
在橢圓上;所以 是方程
是方程 的一個根;
的一個根;
從而; ????????????????????????????????????????? 10分
????????????????????????????????????????? 10分
同理: ;從而直線
;從而直線 的斜率
的斜率 ;
;
又 、
、 ;所以
;所以 ;所以
;所以 所以向量
所以向量 與
與 共線。 14分www.ks5u.com
共線。 14分www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com