
題目列表(包括答案和解析)
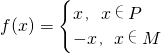 ,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定A={y|y=f(x),x∈P},B={y|y=f(x),x∈M},給出下列三個判斷:
,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定A={y|y=f(x),x∈P},B={y|y=f(x),x∈M},給出下列三個判斷:函數(shù)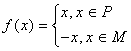 ,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},給出下列四個判斷:
,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},給出下列四個判斷:
①若P∩M=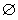 ,則f(P)∩f(M)=
,則f(P)∩f(M)=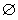 ;②若P∩M≠
;②若P∩M≠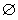 ,則f(P)∩f(M)≠
,則f(P)∩f(M)≠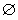 ;
;
③若P∪M=R,則f(P)∪f(M)=R; ④若P∪M≠R,則f(P)∪f(M)≠R;
其中正確判斷有
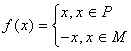 ,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},給出下列四個判斷:
,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M},給出下列四個判斷: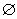 ,則f(P)∩f(M)=
,則f(P)∩f(M)=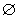 ;②若P∩M≠
;②若P∩M≠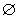 ,則f(P)∩f(M)≠
,則f(P)∩f(M)≠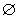 ;
; 函數(shù)![]() ,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定
,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定![]() ,
,![]() ,給出下列四個判斷:
,給出下列四個判斷:
①若![]() ,則
,則![]() ②若
②若![]() ,則
,則![]()
③若![]() ,則
,則![]() ④若
④若![]() ,則
,則![]()
其中正確判斷有
(A)3個 (B)2個 (C)1個 (D) 0個
函數(shù)![]() ,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)=
,其中P、M為實數(shù)集R的兩個非空子集,又規(guī)定f(P)=![]() ,f(M)=
,f(M)=![]() ,則下列四個判斷中正確的有( )
,則下列四個判斷中正確的有( )
①若P∩M=![]() ,則f(P)∩f(M)=
,則f(P)∩f(M)=![]() ②若P∩M¹
②若P∩M¹![]() ,則f(P)∩f(M)¹
,則f(P)∩f(M)¹![]()
③若P∪M=R,則f(P)∪f(M)=R ④若P∪M¹R,則f(P)∪f(M)¹R
A.1個 B.2個 C.3個 D.4個
一、 選擇題:本大題主要考查基本知識和基本運算.每小題5分,滿分40分.
(1)D (2)C (3)A (4)A (5)B (6)D (7)C (8)B
二、填空題:本大題主要考查基本知識和基本運算.每小題5分,滿分30分.
(9)一考試(文史類)(北京卷).files\image229.gif)
(10)一考試(文史類)(北京卷).files\image231.gif)
(11)(0,1),一考試(文史類)(北京卷).files\image233.gif)
(12)一考試(文史類)(北京卷).files\image235.gif)
一考試(文史類)(北京卷).files\image237.gif)
(13)大 -3
(14)3 52
三、解答題:本大題共6小題,共80分.解答應寫出文字說明,證明過程或演算步驟.
(15)本小題主要考查三角恒等變形、三角形面積公式等基本知識,考查運算能力.滿分14分.
解法一:
一考試(文史類)(北京卷).files\image239.gif)
又一考試(文史類)(北京卷).files\image241.gif) ,
,
一考試(文史類)(北京卷).files\image243.gif)
一考試(文史類)(北京卷).files\image245.gif)
一考試(文史類)(北京卷).files\image247.gif) .
.
解法二:
一考試(文史類)(北京卷).files\image249.gif) (1)
(1)
一考試(文史類)(北京卷).files\image251.gif)
一考試(文史類)(北京卷).files\image253.gif) ,
,
一考試(文史類)(北京卷).files\image255.gif) . (2)
. (2)
(1)+(2)得:一考試(文史類)(北京卷).files\image257.gif) .
.
(1)-(2)得:一考試(文史類)(北京卷).files\image259.gif) .
.
一考試(文史類)(北京卷).files\image261.gif) .
.
(以下同解法一)
(16)本小題主要考查直線與平面的位置關系、棱柱等基本知識,考查空間想象能力、邏輯思維能力和運算能力.滿分14分.
解:(I)正三棱柱一考試(文史類)(北京卷).files\image154.gif) 的側(cè)面展開圖是長為6,寬為2的矩形
的側(cè)面展開圖是長為6,寬為2的矩形
其對角線長為一考試(文史類)(北京卷).files\image263.gif) .
.
(II)如圖,將側(cè)面一考試(文史類)(北京卷).files\image265.gif) 繞棱
繞棱一考試(文史類)(北京卷).files\image158.gif) 旋轉(zhuǎn)
旋轉(zhuǎn)一考試(文史類)(北京卷).files\image267.gif) 使其與側(cè)面
使其與側(cè)面一考試(文史類)(北京卷).files\image269.gif) 在同一平面上,點B運動到點D的位置,連接
在同一平面上,點B運動到點D的位置,連接一考試(文史類)(北京卷).files\image271.gif) 交
交一考試(文史類)(北京卷).files\image158.gif) 于M,則
于M,則一考試(文史類)(北京卷).files\image271.gif) 就是由頂點B沿棱柱側(cè)面經(jīng)過棱
就是由頂點B沿棱柱側(cè)面經(jīng)過棱一考試(文史類)(北京卷).files\image158.gif) 到頂點C1的最短路線,其長為
到頂點C1的最短路線,其長為
一考試(文史類)(北京卷).files\image273.gif) .
.
一考試(文史類)(北京卷).files\image275.gif) ,
,一考試(文史類)(北京卷).files\image277.gif) ,
,
故一考試(文史類)(北京卷).files\image279.gif) .
.
一考試(文史類)(北京卷).files\image281.gif)
(III)連接DB,一考試(文史類)(北京卷).files\image283.gif) ,則DB就是平面
,則DB就是平面一考試(文史類)(北京卷).files\image164.gif) 與平面ABC的交線
與平面ABC的交線
在一考試(文史類)(北京卷).files\image285.gif) 中,
中,
一考試(文史類)(北京卷).files\image287.gif)
又一考試(文史類)(北京卷).files\image289.gif) ,
,
由三垂線定理得一考試(文史類)(北京卷).files\image291.gif) .
.
一考試(文史類)(北京卷).files\image293.gif) 就是平面
就是平面一考試(文史類)(北京卷).files\image164.gif) 與平面ABC所成二面角的平面角(銳角),
與平面ABC所成二面角的平面角(銳角),
一考試(文史類)(北京卷).files\image295.gif) 側(cè)面
側(cè)面一考試(文史類)(北京卷).files\image297.gif) 是正方形,
是正方形,
一考試(文史類)(北京卷).files\image299.gif) .
.
故平面一考試(文史類)(北京卷).files\image164.gif) 與平面ABC所成的二面角(銳角)為
與平面ABC所成的二面角(銳角)為一考試(文史類)(北京卷).files\image301.gif) .
.
(17)本小題主要考查直線、拋物線等基本知識,考查運用解析幾何的方法分析問題和解決問題的能力.滿分14分.
解:(I)由已知條件,可設拋物線的方程為一考試(文史類)(北京卷).files\image303.gif) .
.
一考試(文史類)(北京卷).files\image305.gif)
一考試(文史類)(北京卷).files\image295.gif) 點P(1,2)在拋物線上,
點P(1,2)在拋物線上,
一考試(文史類)(北京卷).files\image307.gif) ,得
,得一考試(文史類)(北京卷).files\image309.gif) .
.
故所求拋物線的方程是一考試(文史類)(北京卷).files\image311.gif) ,
,
準線方程是一考試(文史類)(北京卷).files\image313.gif) .
.
(II)設直線PA的斜率為一考試(文史類)(北京卷).files\image315.gif) ,直線PB的斜率為
,直線PB的斜率為一考試(文史類)(北京卷).files\image317.gif) ,
,
則一考試(文史類)(北京卷).files\image319.gif) ,
,一考試(文史類)(北京卷).files\image321.gif) .
.
一考試(文史類)(北京卷).files\image295.gif) PA與PB的斜率存在且傾斜角互補,
PA與PB的斜率存在且傾斜角互補,
一考試(文史類)(北京卷).files\image323.gif) .
.
由A(一考試(文史類)(北京卷).files\image168.gif) ),B(
),B(一考試(文史類)(北京卷).files\image170.gif) )在拋物線上,得
)在拋物線上,得
一考試(文史類)(北京卷).files\image325.gif) ,(1)
,(1)
一考試(文史類)(北京卷).files\image327.gif) ,
(2)
,
(2)
一考試(文史類)(北京卷).files\image329.gif)
由(1)-(2)得直線AB的斜率
一考試(文史類)(北京卷).files\image331.gif)
(18)本小題主要考查函數(shù)、數(shù)列等基本知識,考查分析問題和解決問題的能力.滿分14分.
解:(I)由一考試(文史類)(北京卷).files\image333.gif) ,得
,得一考試(文史類)(北京卷).files\image335.gif) .
.
由一考試(文史類)(北京卷).files\image337.gif) 及
及一考試(文史類)(北京卷).files\image178.gif) ,得
,得一考試(文史類)(北京卷).files\image339.gif) .
.
同理,一考試(文史類)(北京卷).files\image341.gif) .
.
歸納得一考試(文史類)(北京卷).files\image343.gif)
(II)當一考試(文史類)(北京卷).files\image345.gif) 時,
時,一考試(文史類)(北京卷).files\image347.gif) ,
,
一考試(文史類)(北京卷).files\image349.gif) ,
,
一考試(文史類)(北京卷).files\image351.gif) ,
,
一考試(文史類)(北京卷).files\image353.gif) .
.
所以一考試(文史類)(北京卷).files\image136.gif) 是首項為
是首項為一考試(文史類)(北京卷).files\image354.gif) ,公比為
,公比為一考試(文史類)(北京卷).files\image355.gif) 的等比數(shù)列.
的等比數(shù)列.
所以一考試(文史類)(北京卷).files\image357.gif) .
.
(19)本小題主要考查解不等式等基本知識,考查應用數(shù)學知識分析問題和解決問題的能力.滿分12分.
解:(I)列車在B,C兩站的運行誤差(單位:分鐘)分別是
一考試(文史類)(北京卷).files\image359.gif) 和
和一考試(文史類)(北京卷).files\image361.gif)
(II)由于列車在B,C兩站的運行誤差之和不超過2分鐘,所以
一考試(文史類)(北京卷).files\image363.gif) (*)
(*)
當一考試(文史類)(北京卷).files\image365.gif) 時,(*)式變形為
時,(*)式變形為一考試(文史類)(北京卷).files\image367.gif) ,
,
解得一考試(文史類)(北京卷).files\image369.gif) ;
;
當一考試(文史類)(北京卷).files\image371.gif) 時,(*)式變形為
時,(*)式變形為一考試(文史類)(北京卷).files\image373.gif) ,
,
解得一考試(文史類)(北京卷).files\image371.gif) ;
;
當一考試(文史類)(北京卷).files\image375.gif) 時,(*)式變形為
時,(*)式變形為一考試(文史類)(北京卷).files\image377.gif) ,
,
解得一考試(文史類)(北京卷).files\image379.gif)
綜上所述,一考試(文史類)(北京卷).files\image207.gif) 的取值范圍是[39,
的取值范圍是[39,一考試(文史類)(北京卷).files\image381.gif) ].
].
(20)本小題主要考查不等式的證明等基本知識,考查邏輯思維能力、分析問題和解決問題的能力.滿分12分.
解:(I)一考試(文史類)(北京卷).files\image383.gif) .除第N組外的每組至少含有
.除第N組外的每組至少含有一考試(文史類)(北京卷).files\image385.gif) 個數(shù).
個數(shù).
(II)當?shù)趎組形成后,因為一考試(文史類)(北京卷).files\image387.gif) ,所以還有數(shù)沒分完,這時余下的每個數(shù)必大于余差
,所以還有數(shù)沒分完,這時余下的每個數(shù)必大于余差一考試(文史類)(北京卷).files\image223.gif) ,余下數(shù)之和也大于第n組的余差
,余下數(shù)之和也大于第n組的余差一考試(文史類)(北京卷).files\image223.gif) ,即
,即
一考試(文史類)(北京卷).files\image389.gif) ,
,
由此可得一考試(文史類)(北京卷).files\image391.gif) .
.
因為一考試(文史類)(北京卷).files\image393.gif) ,所以
,所以一考試(文史類)(北京卷).files\image225.gif) .
.
(III)用反證法證明結(jié)論,假設一考試(文史類)(北京卷).files\image395.gif) ,即第11組形成后,還有數(shù)沒分完,由(I)和(II)可知,余下的每個數(shù)都大于第11組的余差
,即第11組形成后,還有數(shù)沒分完,由(I)和(II)可知,余下的每個數(shù)都大于第11組的余差一考試(文史類)(北京卷).files\image397.gif) ,且
,且一考試(文史類)(北京卷).files\image399.gif) ,
,
故余下的每個數(shù)一考試(文史類)(北京卷).files\image401.gif) . (*)
. (*)
因為第11組數(shù)中至少含有3個數(shù),所以第11組數(shù)之和大于一考試(文史類)(北京卷).files\image403.gif) ,
,
此時第11組的余差一考試(文史類)(北京卷).files\image405.gif) ,
,
這與(*)式中一考試(文史類)(北京卷).files\image407.gif) 矛盾,所以
矛盾,所以一考試(文史類)(北京卷).files\image227.gif) .
.
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com