題目列表(包括答案和解析)
某中學開展“創建文明城市知識競賽”活動，競賽題由20道選擇題構成，每道選擇題有4個選項，其中有且只有1個選項是正確的，要求學生在規定時間內通過筆試完成，且每道題必須選出一個選項（不得多選和不選），每道題選擇正確得6分，選擇錯誤得0分.已知學生甲對任一道題選擇正確的概率是
；學生乙由于未做準備，因此只能從每道題的4個選項中隨機地選擇1個.
（1）比較甲得66分的概率與乙得54分的概率的大小；
（2）就前兩道題而言，求甲、乙兩人得分之和不得低于18分的概率.
| 3 | 4 |
某中學開展的“我為四川地震災區獻愛心”捐書活動中，校團委為了了解九年級同學的捐書情況，用簡單的隨機抽樣方法從高一年級的10個班中抽取50名同學，對這50名同學所捐的書進行分類統計后，繪制了如下統計表：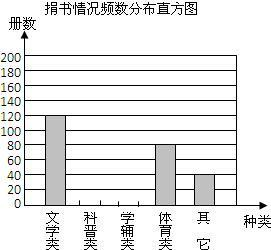
（1）在下圖中，補全這50名同學捐書情況的頻數分布直方圖；
| 社團 | 相關人數 | 抽取人數 |
| 文學 | 24 | a |
| 街舞 | 18 | 3 |
| 魔術 | b | 5 |
| 羽毛球 | 12 | c |
一、選擇題
BDCBB DCBCB AA
二、填空題
13．300 14．（文）
（理）3 15．
16．①③④
三、解答題
17．解：（1）
，
且與向量
又
，
（2）由（1）可得A+C
，
8分
10分
，
當且僅當
時，
12分
18．（文科）解：設既會唱歌又會跳舞的有x人，則文娛隊共有（7－x）人，那么只會一項的人數是（7－2x）人，
（1）
即
故文娛隊共有5人。（8分）
（2）P（
=1）
（12分）
（理科）解：（1）甲得66分（正確11題）的概率為
……………………2分
乙得54分（正確9題）的概率為
………………4分
顯然P1=P2，即甲得66分的概率與乙得54分的概率一樣大。………………6分
（2）設答錯一題倒扣x分，則學生乙選對題的個數為
隨機選擇20個題答對題的個數的期望為
，
得分為
，=6
令
即每答錯一題應該倒扣2分。……………………12分
19．解（1）取BD中點N，連AN、MN
∵MN//BC
∴∠AMN或其鄰補角就是異面直線AM與BC所成的角，在△AMN中，
（4分）
（2）取BE中點P，連AP、PM，作MQ⊥AP于Q，
過Q作QH⊥AB于H，連MH，
∵EB⊥AP，EB⊥PM
∵EB⊥面APM即EB⊥MQ，
∴MQ⊥面AEB
∴HQ為MH在面AEB上的射影，即MH⊥AB
∴∠MHQ為二面角M―AB―E的平面角，
在△AMO中，
在△ABP中，
∴二面角M―AB―E的大小，為
（8分）
（3）若將圖（1）與圖（2）面ACD重合，該幾何體是5面體
這斜三棱柱的體積=3VA-BCD=
（12分）
20．（文科）（1）
，
即
…………………………2分
……………………4分
當
恒成立，
的單調區間為
當
…………………………6分
此時，函數
上是增函數，
在
上是減函數……………………8分
（2）
直線
的斜率為－4………………9分
假設
無實根
不可能是函數圖象的切線。………………12分
（理科）（1）
由于A、B、C三點共線，
即
……………………2分
故
…………………………4分
（2）令
由
上是增函數……………………6分
故
即
………………………………8分
（3）原不等式等價于
令
………………10分
當
令
得
12分
21．解：（I）由
因直線
故所求橢圓方程為
（II）當L與x軸平行時，以AB為直徑的圓的方程：
當L與y軸平行時，以AB為直徑的圓 的方程：
即兩圓相切于點（0，1）
因此，所求的點T如果存在，只能是（0，1）。事實上，點T（0，1）就是所求的點，證明如下。
若直線L垂直于x軸時，以AB為直徑的圓過點T（0，1）
若直線L不垂直于x軸時，可設直線
由
記點
又因為
所以
，即以AB為直徑的圓恒過點T（0，1），故在坐標平面上存在一個定點T（0，1）滿足條件
22．（文科）解：（I）
曲線C在點
（2分）
令
依題意點
又
（4）
（5分）
（II）由已知
①
②
①-②得
（9分）
（10分）
又
又當
（13）
綜上
（14分）
22．（理科）解：（I）
2
（II）
3分
4分
上是增函數 5分
又當
也是單調遞增的 6分
當
此時，
不一定是增函數 7分
（III）當
當
欲證：
即證：
即需證：
猜想
………………8分
構造函數
在（0，1）上時單調遞減的，
……………………10分
設
，
同理可證
成立……………………12分
分別取
，所以n-1個不等式相加即得：
……………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com