
題目列表(包括答案和解析)
已知等差數列{an}的首項為4,公差為4,其前n項和為Sn,則數列 {![]() }的前n項和為( )
}的前n項和為( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考點: | 數列的求和;等差數列的性質. |
| 專題: | 等差數列與等比數列. |
| 分析: | 利用等差數列的前n項和即可得出Sn,再利用“裂項求和”即可得出數列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴數列 { 故選A. |
| 點評: | 熟練掌握等差數列的前n項和公式、“裂項求和”是解題的關鍵. |
定義方程![]() 的實數根
的實數根![]() 叫做函數
叫做函數![]() 的“新駐點”,若函數
的“新駐點”,若函數![]()
![]()
![]() 的“新駐點”分別為
的“新駐點”分別為![]() ,則
,則![]() 的大小關系為 ▲ 。
的大小關系為 ▲ 。
〖提示:![]() 〗
〗
定義方程![]() 的實數根
的實數根![]() 叫做函數
叫做函數![]() 的“新駐點”,若函數
的“新駐點”,若函數![]()
![]()
![]() 的“新駐點”分別為
的“新駐點”分別為![]() ,則
,則![]() 的大小關系為 ▲ 。
的大小關系為 ▲ 。
〖提示:![]() 〗
〗
下列函數中,既是偶函數,又是在區間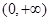 上單調遞減的函數為〖答〗( )
上單調遞減的函數為〖答〗( )
A 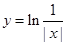 B
B 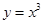 C
C
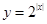 D
D
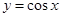
下列函數中,既是偶函數,又是在區間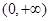 上單調遞減的函數為〖答〗( )
上單調遞減的函數為〖答〗( )
A 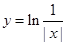 B
B 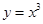 C
C 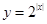 D
D 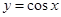
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com