題目列表(包括答案和解析)
已知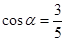
，
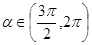，求
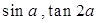的值
【解析】本試題主要考查了三角函數的二倍角公式的運用。利用同角三角函數關系式可知
，所以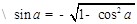
，再利用二倍角正切公式
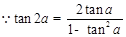得到結論。
解：（Ⅰ）
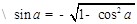
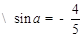
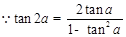
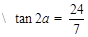
【2012高考江蘇26】（10分）設集合
，
．記
為同時滿足下列條件的集合
的個數：
①
；②若
，則
；③若
，則
。
（1）求
；
（2）求的解析式（用
表示）．
已知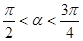
，
,
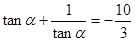（Ⅰ）求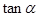
的值；
（Ⅱ）求
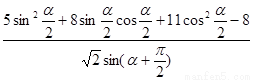的值。
【解析】第一問中，因為，∴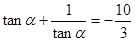
∴
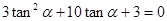
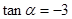或
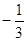又∴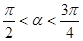
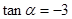
第二問中原式=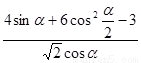
=
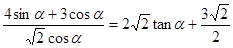進而得到結論。
（Ⅰ）解：∵∴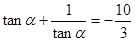
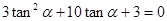
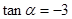∴或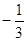……………………………………3分
又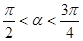∴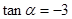……………………………2分
(Ⅱ) 解：原式=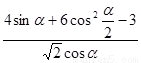 ……………………2分
=
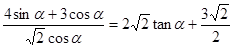…………2分
=
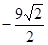
設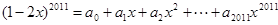
，求下列各式的值：
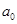(Ⅰ)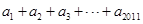 
;
（Ⅱ）
； （Ⅲ）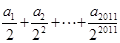
.
【解析】本試題主要考查了二項式定理的運用。第一問中利用賦值的思想，令x=0，得到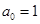
第二問中，利用令x=1，得到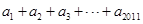
第三問中，利用令x=1/2，得到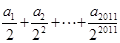
解：（1）令x=0，得到；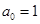
（2）令x=1，得到
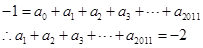
（3）令x=1/2，得到
已知
，求下列各式的值：
（1）
（2）
【解析】本試題主要考查了同角三角函數關系式的運用。第一問中利用將分子分母同時除以
得，原式=
第二問中，構造分式表達式，原式=
=
=
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com