
題目列表(包括答案和解析)
已知![]() .
.
⑴ 求函數(shù)![]() 在
在![]() 上的最小值;
上的最小值;
⑵ 對一切![]() ,
,![]() 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
已知![]() .
.
(Ⅰ)求函數(shù)![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅱ)對一切![]() 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(Ⅲ)證明:對一切![]() ,都有
,都有![]() 成立.
成立.
已知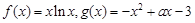 .
.
(1) 求函數(shù)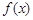 在
在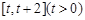 上的最小值;
上的最小值;
(2) 對一切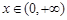 ,
,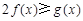 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(3) 證明:對一切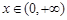 ,都有
,都有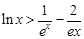 成立.
成立.
已知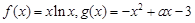 .
.
(1) 求函數(shù)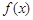 在
在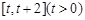 上的最小值;
上的最小值;
(2) 對一切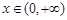 ,
,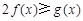 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(3) 證明:對一切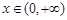 ,都有
,都有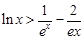 成立.
成立.
已知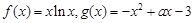 .
.
(1) 求函數(shù)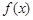 在
在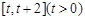 上的最小值;
上的最小值;
(2) 對一切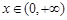 ,
,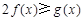 恒成立,求實數(shù)a的取值范圍;
恒成立,求實數(shù)a的取值范圍;
(3) 證明:對一切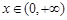 ,都有
,都有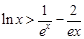 成立.
成立.
一、填空題:
1. 考-數(shù)學.files/image172.gif) 2. 三 3. 1 4. 25 5.
2. 三 3. 1 4. 25 5. 考-數(shù)學.files/image174.gif) 6. -1 7.
6. -1 7. 考-數(shù)學.files/image176.gif) 8. (1,0)
8. (1,0)
9. 考-數(shù)學.files/image178.gif) 10. 8 11. 1 12. (0,2) 13. 2026 14. ①②③
10. 8 11. 1 12. (0,2) 13. 2026 14. ①②③
二、解答題:
15. 解:(1)因為考-數(shù)學.files/image180.gif) ,
,考-數(shù)學.files/image182.gif) ,所以
,所以
考-數(shù)學.files/image184.gif) …………………………4分
…………………………4分
考-數(shù)學.files/image186.gif) ……………………………………………………..6分
……………………………………………………..6分
因此,當考-數(shù)學.files/image188.gif) ,即
,即考-數(shù)學.files/image190.gif) (
(考-數(shù)學.files/image192.gif) )時,
)時,考-數(shù)學.files/image114.gif) 取得最大值
取得最大值考-數(shù)學.files/image195.gif) ;…8分
;…8分
(2)由考-數(shù)學.files/image197.gif) 及
及考-數(shù)學.files/image199.gif) 得
得考-數(shù)學.files/image201.gif) ,兩邊平方得
,兩邊平方得
考-數(shù)學.files/image203.gif) ,即
,即考-數(shù)學.files/image205.gif) .……………………………………………12分
.……………………………………………12分
因此,考-數(shù)學.files/image207.gif) .……………………………14分
.……………………………14分
16.解:由已知不等式得
考-數(shù)學.files/image209.gif) ①
①
或 考-數(shù)學.files/image211.gif) ②
②
不等式①的解為考-數(shù)學.files/image213.gif)
考-數(shù)學.files/image215.gif)
不等式②的解為考-數(shù)學.files/image217.gif) 或
或考-數(shù)學.files/image219.gif)
考-數(shù)學.files/image215.gif) …………………………………………………4分
…………………………………………………4分
因為,對考-數(shù)學.files/image217.gif) 或
或考-數(shù)學.files/image213.gif) 或
或考-數(shù)學.files/image219.gif) 時,P是正確的
時,P是正確的考-數(shù)學.files/image215.gif) ………………………..6分
………………………..6分
對函數(shù)考-數(shù)學.files/image124.gif) 求導
求導考-數(shù)學.files/image222.gif) …8分
…8分
令考-數(shù)學.files/image224.gif) ,即
,即考-數(shù)學.files/image226.gif)
考-數(shù)學.files/image215.gif)
當且僅當D>0時,函數(shù)f(考-數(shù)學.files/image089.gif) )在(-¥,+¥)上有極值
)在(-¥,+¥)上有極值考-數(shù)學.files/image215.gif)
由考-數(shù)學.files/image229.gif) 得
得考-數(shù)學.files/image231.gif) 或
或考-數(shù)學.files/image233.gif) ,
,
因為,當考-數(shù)學.files/image231.gif) 或
或考-數(shù)學.files/image233.gif) 時,Q是正確的
時,Q是正確的考-數(shù)學.files/image215.gif) ………………………………………………12分
………………………………………………12分
綜上,使P正確且Q正確時,實數(shù)m的取值范圍為(-¥,-1)È考-數(shù)學.files/image236.gif)
考-數(shù)學.files/image215.gif) ……….14分
……….14分
17.解:(1)因為函數(shù)考-數(shù)學.files/image126.gif) 的圖象關(guān)于原點對稱,所以
的圖象關(guān)于原點對稱,所以考-數(shù)學.files/image238.gif) 即
即考-數(shù)學.files/image240.gif) ,
,
考-數(shù)學.files/image242.gif) ,得
,得考-數(shù)學.files/image244.gif) 或
或考-數(shù)學.files/image246.gif) ……………………………………….2分
……………………………………….2分
當考-數(shù)學.files/image248.gif) 時,
時,考-數(shù)學.files/image250.gif) 舍去;
舍去;
當考-數(shù)學.files/image246.gif) 時,
時,考-數(shù)學.files/image253.gif) ,令
,令考-數(shù)學.files/image255.gif) ,解得
,解得考-數(shù)學.files/image257.gif) 或
或考-數(shù)學.files/image259.gif) .
.
所以符合條件的m值為-1 …………………………………………………………………4分
(2)由(1)得考-數(shù)學.files/image261.gif) ,任取
,任取考-數(shù)學.files/image263.gif) ,
,
考-數(shù)學.files/image265.gif)
考-數(shù)學.files/image267.gif) ……………………6分
……………………6分
考-數(shù)學.files/image269.gif) ∴
∴考-數(shù)學.files/image271.gif) ,
,
∴考-數(shù)學.files/image273.gif) ………………………………………………………………….8分
………………………………………………………………….8分
∴當考-數(shù)學.files/image275.gif) 時,
時,考-數(shù)學.files/image277.gif) 即
即考-數(shù)學.files/image279.gif) ,此時
,此時考-數(shù)學.files/image027.gif) 為增函數(shù);
為增函數(shù);
當考-數(shù)學.files/image282.gif) 時,
時,考-數(shù)學.files/image284.gif) 即
即考-數(shù)學.files/image286.gif) ,此時
,此時考-數(shù)學.files/image027.gif) 為減函數(shù)…10分
為減函數(shù)…10分
(3)由(2)知,當考-數(shù)學.files/image282.gif) 時
時考-數(shù)學.files/image027.gif) 在
在考-數(shù)學.files/image133.gif) 上為減函數(shù);同理在
上為減函數(shù);同理在考-數(shù)學.files/image290.gif) 上也為減函數(shù)
上也為減函數(shù)
當考-數(shù)學.files/image292.gif) 時,
時,考-數(shù)學.files/image294.gif) 與已知矛盾,舍去;………………12分
與已知矛盾,舍去;………………12分
當考-數(shù)學.files/image296.gif) 時,因為函數(shù)
時,因為函數(shù)考-數(shù)學.files/image027.gif) 的值域為
的值域為考-數(shù)學.files/image133.gif)
∴考-數(shù)學.files/image298.gif) 且
且考-數(shù)學.files/image300.gif) ,解得
,解得考-數(shù)學.files/image302.gif) ,
,考-數(shù)學.files/image304.gif) ……………………………………14分
……………………………………14分
18.解:(1)由考-數(shù)學.files/image306.gif) ,令
,令考-數(shù)學.files/image308.gif) ,則
,則考-數(shù)學.files/image310.gif) ,又
,又考-數(shù)學.files/image312.gif) ,所以
,所以考-數(shù)學.files/image314.gif) .
.
考-數(shù)學.files/image316.gif) ,則
,則考-數(shù)學.files/image318.gif) . …………………………………………………………………………………….2分
. …………………………………………………………………………………….2分
當考-數(shù)學.files/image320.gif) 時,由
時,由考-數(shù)學.files/image306.gif) ,可得
,可得考-數(shù)學.files/image322.gif) . 即
. 即考-數(shù)學.files/image324.gif) ..6分
..6分
所以考-數(shù)學.files/image139.gif) 是以
是以考-數(shù)學.files/image314.gif) 為首項,
為首項,考-數(shù)學.files/image328.gif) 為公比的等比數(shù)列,于是
為公比的等比數(shù)列,于是考-數(shù)學.files/image330.gif) . ……8分
. ……8分
(2)數(shù)列考-數(shù)學.files/image147.gif) 為等差數(shù)列,公差
為等差數(shù)列,公差考-數(shù)學.files/image333.gif) ,可得
,可得考-數(shù)學.files/image335.gif) . ….10分
. ….10分
從而考-數(shù)學.files/image337.gif) . ……………………………………………..12分
. ……………………………………………..12分
∴考-數(shù)學.files/image339.gif)
考-數(shù)學.files/image341.gif) ……….16分
……….16分
19.解:(1)依題意知汽車從甲地勻速行駛到乙地所用時間為考-數(shù)學.files/image343.gif) ,全程運輸成本為
,全程運輸成本為考-數(shù)學.files/image345.gif) ……………………………………….4分
……………………………………….4分
故所求函數(shù)及其定義域為考-數(shù)學.files/image347.gif) ………………………….6分
………………………….6分
(2)依題意知a,v都為正數(shù),故有考-數(shù)學.files/image349.gif)
當且僅當考-數(shù)學.files/image351.gif) .即
.即考-數(shù)學.files/image353.gif) 時上式中等號成立………………………...8分
時上式中等號成立………………………...8分
(1)若考-數(shù)學.files/image355.gif) ,即
,即考-數(shù)學.files/image357.gif) 時則當
時則當考-數(shù)學.files/image353.gif) 時,全程運輸成本y最小.10分
時,全程運輸成本y最小.10分
(2)若考-數(shù)學.files/image359.gif) ,即
,即考-數(shù)學.files/image361.gif) 時,則當
時,則當考-數(shù)學.files/image363.gif) 時,有
時,有
考-數(shù)學.files/image365.gif)
考-數(shù)學.files/image367.gif) .
.
考-數(shù)學.files/image369.gif) 。也即當v=100時,全程運輸成本y最小.…….14分
。也即當v=100時,全程運輸成本y最小.…….14分
綜上知,為使全程運輸成本y最小,當考-數(shù)學.files/image357.gif) 時行駛速度應(yīng)為
時行駛速度應(yīng)為考-數(shù)學.files/image353.gif) 千米/時;
千米/時;
當考-數(shù)學.files/image361.gif) 時行駛速度應(yīng)為v=
時行駛速度應(yīng)為v=
20.解: (1) 考-數(shù)學.files/image371.gif) ,當
,當考-數(shù)學.files/image373.gif) ,
,考-數(shù)學.files/image375.gif) ,
,考-數(shù)學.files/image114.gif) 單調(diào)遞減,當
單調(diào)遞減,當考-數(shù)學.files/image377.gif) ,
,考-數(shù)學.files/image379.gif) ,
,考-數(shù)學.files/image114.gif) 單調(diào)遞增.………………………………………………………………..2分
單調(diào)遞增.………………………………………………………………..2分
① 考-數(shù)學.files/image381.gif) ,t無解;
,t無解;
② 考-數(shù)學.files/image383.gif) ,即
,即考-數(shù)學.files/image385.gif) 時,
時,考-數(shù)學.files/image387.gif) ;
;
③ 考-數(shù)學.files/image389.gif) ,即
,即考-數(shù)學.files/image391.gif) 時,
時,考-數(shù)學.files/image114.gif) 在
在考-數(shù)學.files/image393.gif) 上單調(diào)遞增,
上單調(diào)遞增,考-數(shù)學.files/image395.gif) ;
;
所以考-數(shù)學.files/image397.gif) .…………………………………………………………..6分
.…………………………………………………………..6分
(2) 考-數(shù)學.files/image399.gif) ,則
,則考-數(shù)學.files/image401.gif) ,………………………………………..8分
,………………………………………..8分
設(shè)考-數(shù)學.files/image403.gif) ,則
,則考-數(shù)學.files/image405.gif) ,
,考-數(shù)學.files/image407.gif) ,
,考-數(shù)學.files/image409.gif) ,
,考-數(shù)學.files/image411.gif) 單調(diào)遞減,
單調(diào)遞減,考-數(shù)學.files/image413.gif) ,
,考-數(shù)學.files/image415.gif) ,
,考-數(shù)學.files/image411.gif) 單調(diào)遞增,所以
單調(diào)遞增,所以考-數(shù)學.files/image417.gif) ……………………….10分
……………………….10分
因為對一切考-數(shù)學.files/image166.gif) ,
,考-數(shù)學.files/image419.gif) 恒成立,所以
恒成立,所以考-數(shù)學.files/image421.gif) ;………………..12分
;………………..12分
(3) 問題等價于證明考-數(shù)學.files/image423.gif) ,由⑴可知
,由⑴可知考-數(shù)學.files/image425.gif) 的最小值是
的最小值是考-數(shù)學.files/image427.gif) ,當且僅當
,當且僅當考-數(shù)學.files/image429.gif) 時取到………………………………………………………….14分
時取到………………………………………………………….14分
設(shè)考-數(shù)學.files/image431.gif) ,則
,則考-數(shù)學.files/image433.gif) ,易得
,易得考-數(shù)學.files/image435.gif) ,當且僅當
,當且僅當考-數(shù)學.files/image437.gif) 時取到,從而對一切
時取到,從而對一切考-數(shù)學.files/image166.gif) ,都有
,都有考-數(shù)學.files/image170.gif) 成立.……………………………..16分
成立.……………………………..16分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com