
題目列表(包括答案和解析)
| y |
| x+2 |
| SM |
| SN |
A、5
| ||
B、
| ||
C、15
| ||
D、5+10
|
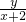 的取值范圍;
的取值范圍;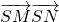 的最小值.
的最小值.| y |
| x+2 |
| SM |
| SN |
一、選擇題
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
答案
C
B
C
D
C
A
C
B
A
D
C
提示與分析:
1. ,故選C。
,故選C。
2.易知p成立,m<3,q成立,2<m< ,從而p成立
,從而p成立 成立,故選B。
成立,故選B。
3.選C
4.由已知得 即
即 ,得
,得 ,故選D。
,故選D。
5.易知 ,故選C。
,故選C。
6. ,作圖知選A。
,作圖知選A。
7.選C。由題: 。
。
8.設(shè)球半徑為R,由 ,由
,由 知,三棱錐頂點(diǎn)S愛(ài)底面ABC內(nèi)的攝影D是△ABC的外心,又∠ACB=90°,∴D是AB的中點(diǎn),點(diǎn)O到ABC的距離h=OD,設(shè)SA=SB=SC=AB=2
知,三棱錐頂點(diǎn)S愛(ài)底面ABC內(nèi)的攝影D是△ABC的外心,又∠ACB=90°,∴D是AB的中點(diǎn),點(diǎn)O到ABC的距離h=OD,設(shè)SA=SB=SC=AB=2 ,可得
,可得
 ,或h=10(舍),故選B。
,或h=10(舍),故選B。
9.由題設(shè)易知M是PF的中點(diǎn),設(shè)橢圓右焦點(diǎn)為 ,由
,由 知,
知, =8,
=8, ,又易知該橢圓的離心率
,又易知該橢圓的離心率 ,再由橢圓第二定義得,點(diǎn)P到橢圓左準(zhǔn)線(xiàn)的距離
,再由橢圓第二定義得,點(diǎn)P到橢圓左準(zhǔn)線(xiàn)的距離 ,故選A。
,故選A。
10.由 ,∴
,∴ 故選D。
故選D。
11.由題設(shè)知 是周期為2的周期函數(shù),由
是周期為2的周期函數(shù),由 時(shí),
時(shí), ,可作出
,可作出 再R上的簡(jiǎn)圖,又
再R上的簡(jiǎn)圖,又 是偶函數(shù),再作出簡(jiǎn)圖,則可確定兩圖像的交點(diǎn)個(gè)數(shù),故選C。
是偶函數(shù),再作出簡(jiǎn)圖,則可確定兩圖像的交點(diǎn)個(gè)數(shù),故選C。
二、填空題
12.112 13.9 14.32 15.①②④
提示與分析:
12.令 得
得 ,再分別令
,再分別令 得兩式,再相加可得
得兩式,再相加可得 ,從而得知
,從而得知 。
。
13.由題得: ,
, 得:
得: ,而
,而 可看作是單位圓上的點(diǎn)(m,n)到點(diǎn)(2,0)的距離,則易知,
可看作是單位圓上的點(diǎn)(m,n)到點(diǎn)(2,0)的距離,則易知, 的最大值為9.
的最大值為9.
14.由題設(shè)知, 又0<q<1則得
又0<q<1則得 ,∴
,∴
15.如圖,①知直線(xiàn)BC與面 所成的角即為∠
所成的角即為∠ ,故①正確。
,故①正確。
②易知四面體 在四個(gè)側(cè)面的攝影圖形面積均最小,為正方形面積之半,故②正確
在四個(gè)側(cè)面的攝影圖形面積均最小,為正方形面積之半,故②正確
③點(diǎn)M到平面 的距離,即為點(diǎn)
的距離,即為點(diǎn) 到平面
到平面 的距離。其等于
的距離。其等于 ,故③不正確。
,故③不正確。
④易知BM與 所成的角,即為BM與
所成的角,即為BM與 所成的角,設(shè)∠
所成的角,設(shè)∠ ∠
∠ 易知
易知 ,
, ,即
,即 ,故④正確。
,故④正確。
三、解答題
16.(1)由題設(shè)知:
再由余弦定理得:
當(dāng)且僅當(dāng) 時(shí)取等號(hào),故所求B的取值范圍是
時(shí)取等號(hào),故所求B的取值范圍是 (3分)
(3分)
(2)∵ ,∴
,∴ ,
,
∴0<b ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng) 時(shí),
時(shí),
∴
∴ (6分)
(6分)
(3)由(1)(2)易知,當(dāng)△ABC的面積S最大時(shí),△ABC是邊長(zhǎng)為2的正△,此時(shí)易知 ∠
∠ ∠
∠
 在△AGM中,由正弦定理得:
在△AGM中,由正弦定理得:
則
在△AGN中,同理可得:
 (10分)
(10分)
∴ (或用降次公式化簡(jiǎn))
(或用降次公式化簡(jiǎn))


 (12分)
(12分)
17.解法一:
(1)由PB⊥面ABCD,CD⊥PD知CD⊥BD
 在直角梯形ABCD中,AD⊥AB,AB=AD=3,
在直角梯形ABCD中,AD⊥AB,AB=AD=3,
∴BD= ,BC=6
,BC=6
取BC的中點(diǎn)F,連結(jié)AF,則AF∥CD,
∴PA與CD所成的角就是∠PAF (4分)
連PF由題設(shè)易知AF=PF=PA= ,
,
∴∠PAF=60°即為所求 (6分)
(2)連AC交BD于G,連EG,易知 ,
,
又 ∴
∴ ,∴PC∥EG,又EG
,∴PC∥EG,又EG 面EBD,∴PC∥面EBD (10分)
面EBD,∴PC∥面EBD (10分)
(3)∵PB⊥面ABCD,∴AD⊥PB,
又AD⊥AB,∴AD⊥面EAB
作AH⊥BE于H,連DH,則DH⊥BE, (12分)
在△AEB中,易求得BE= ,
,
在 △DAH中,
△DAH中, ∠
∠
即所求二面角的大小為 (14分)
(14分)
 解法二:(1)如圖建立空間直角坐標(biāo)系
解法二:(1)如圖建立空間直角坐標(biāo)系 ,設(shè)
,設(shè)

則A(0,3,0),P(0,0,3)D(3,3,0),C( ,0,0),
,0,0), =
=
∵ ,∴
,∴ ,
,
即:3(3- )+9=0
)+9=0 (2分)
(2分)
∴
∴
∴ ,即異面直線(xiàn)PA與CD所成的交為60°
(6分)
,即異面直線(xiàn)PA與CD所成的交為60°
(6分)
(2)設(shè)平面BED的法向量為 ∵
∵
由 得
得
 ,∴
,∴ (12分)
(12分)
又由(1)知 ,∴
,∴ ,∴PC∥面EBD (10分)
,∴PC∥面EBD (10分)
(3)由(2)知
又平面ABE的法向量 ,
,
故所求二面角的大小為 (14分)
(14分)
18.(1)在第一環(huán)節(jié)中,乙選手從6道題目中任選3道至少有1道操作題的概率
 (4分)
(4分)
(2)在第二環(huán)節(jié)中,甲搶到的題目多于乙選手而不多于丙選手的情況有以下三種:
甲、乙、丙三位選手搶到的題目的個(gè)數(shù)分別為1,0,4;2,0,3;2,1,2,
故所求的概率


(8分)
(3)在第三個(gè)環(huán)節(jié)中,就每一次答題而言,丙選手得分是一個(gè)隨機(jī)變量 ,
,
若選A類(lèi)題,其得分的期望是 (分)
(分)
若選B類(lèi)題,其得分的期望是 (分)
(分)
若選C類(lèi)題,其得分的期望是 (分)
(分)
由于 >
> =
= ,故丙應(yīng)選B類(lèi)得分的切望值更大。(12分)
,故丙應(yīng)選B類(lèi)得分的切望值更大。(12分)
19.(1)依題意可得:
(4分)
(2)由

當(dāng) 時(shí),
時(shí), ,則
,則
∴ ,∴
,∴
即第 次操作后溶液的濃度為
次操作后溶液的濃度為 (9分)
(9分)
(3)由(2)可得:
則
由錯(cuò)位相減法可求得:

故所求 (13分)
(13分)
20.(1)由 <0,
<0, >
> ,∴
,∴
又 >
> <
< ,∴
,∴
從而有  (4分)
(4分)
(2)由(1)可知,
故 ,則
,則
令 >
> ∵
∵ >
> 得
得 >
> ,∴
,∴ >
>
令 <
< ∵
∵ >
> ,解得
,解得 <
< <
<
列表:

(0,1)
1
(1,+∞)

-
0
+

↓
0
↑
即  在
在 處有最小值0 (8分)
處有最小值0 (8分)
(3)由 易知
易知 時(shí),
時(shí), <
<
∴ 為減函數(shù),其最小值為1
為減函數(shù),其最小值為1
令 在
在 上單增,其最大值為
上單增,其最大值為
依題意得:
又 >
> ∴
∴ <
< (14分)
(14分)
21.(1)由題設(shè)及平面幾何知識(shí)得: <
< ,
,
∵動(dòng)點(diǎn)P的軌跡是以A、B為交點(diǎn)的雙曲線(xiàn)右支,
由
故所求P點(diǎn)的軌跡方程為: (4分)
(4分)
(2)易知 直線(xiàn) 恒過(guò)雙曲線(xiàn)焦點(diǎn)B(3,0)
恒過(guò)雙曲線(xiàn)焦點(diǎn)B(3,0)
設(shè)該直線(xiàn)與雙曲線(xiàn)右支相交于
由雙曲線(xiàn)第二定義知,
又 ∴
∴ ,則
,則 ,
,
由 得
得 ,從而易知,僅當(dāng)
,從而易知,僅當(dāng) 時(shí),
時(shí), 滿(mǎn)足
滿(mǎn)足
故所求 (8分)
(8分)
(3)設(shè) ,且p分有向線(xiàn)段
,且p分有向線(xiàn)段 所成的比為
所成的比為 ,
,
則 ,
, ,
,
又點(diǎn) 在雙曲線(xiàn)
在雙曲線(xiàn) 上,∴
上,∴
化簡(jiǎn)得:
又

∴ (11分)
(11分)
令
∵ 在
在 上單減,在
上單減,在 上單增,
上單增,
又 ,∴
,∴ 在
在 上單減,在
上單減,在 上單增,∴
上單增,∴
又
 ,∴
,∴
故所求 的最小值為9,最大值為
的最小值為9,最大值為 。 (14分)
。 (14分)
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有
天星教育網(wǎng)(www.tesoon.com) 版權(quán)所有