
2009年云南省曲靖一中高考沖刺卷文科數學 (五)
(五)
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,滿分150分,考試時間120分鐘.
第Ⅰ卷(選擇題,共60分)
一、選擇題:本大題共12小題.每小題5分,共60分.在每小題給出的四個選項中,只
有一項是符合題目要求的.
1.已知集合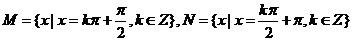 ,則
,則
A.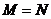 B.
B. C.
C.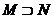 D.
D.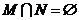

2.已知函數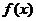 是定義在
是定義在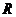 上的奇函,當
上的奇函,當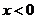 時,
時,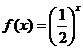 ,那么
,那么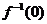 的值
的值
為
A.2 B.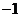 C.0 D.
C.0 D.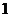

3.函數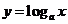 在
在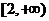 上恒有
上恒有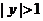 ,則實數
,則實數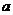 的取值范圍是
的取值范圍是
A.(1,2) B.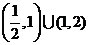

C.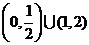 D.
D.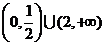

4.已知直線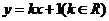 與橢圓
與橢圓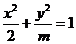 總有交點,則m的取值范圍為
總有交點,則m的取值范圍為
A.(1,2] B.[1,2)
C.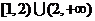 D.
D.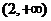

5.從5名羽毛球隊員中選3人參加團體比賽,其中甲在乙之前出場的概率為
A.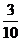 B.
B.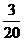 C.
C.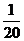 D.
D.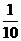

6.已知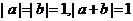 ,則
,則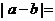

A.1 B.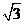 C.
C.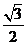 D.2
D.2
7.已知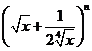 的展開式前三項的系數成等差數列,則展開式中有理項的個數是
的展開式前三項的系數成等差數列,則展開式中有理項的個數是
A.1 B.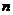 有關
有關
8.使函數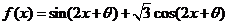 是奇函數,且在
是奇函數,且在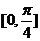 上是減函數的
上是減函數的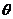 的
的 
一個值是
A.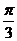 B.
B.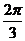 C.
C.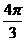 D.
D.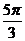

9.已知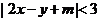 表示的平面區域包含點(0,0)和(
表示的平面區域包含點(0,0)和(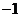 ,1),則
,1),則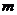 的取值范圍是
的取值范圍是
A.(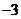 ,6) B.(0,6) C.(0,3) D.(
,6) B.(0,6) C.(0,3) D.(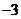 ,3)
,3)
10.橢圓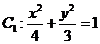 的左準線為
的左準線為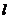 ,左、右焦點分別為
,左、右焦點分別為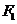 、
、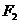 ,拋物線
,拋物線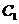 的準線為
的準線為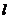 ,
,
焦點是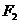 ,
,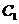 與
與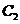 的一個交點為
的一個交點為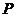 ,則
,則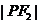 的值等于
的值等于
A.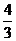 B.
B.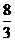 C.4 D.8
C.4 D.8
11.一副撲克牌去掉兩張王后還有52張,將牌發給4個人,每人13張,則某人獲得的13
張牌中花色齊全的全部情況數為
A. B.
B.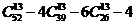

C.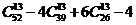 D.
D.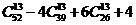

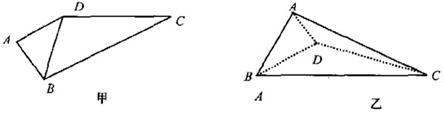
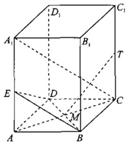
12.如圖甲所示,四邊形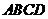 中,
中,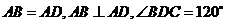 ,將
,將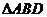 沿
沿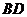

折起,使平面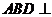 平面
平面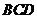 ,構成三棱錐
,構成三棱錐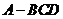 ,如圖乙所示,則二面角
,如圖乙所示,則二面角
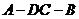 的正切值為
的正切值為
A.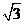 B.
B.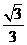 C.
C.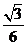 D.
D.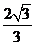




第Ⅱ卷(非選擇題,共90分)
二、填空題:本大題共4小題,每小題5分,共20分.把答案填在題中橫線上.
13.不等式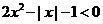 的解集是
.
的解集是
.
14.已知過球面上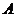 、
、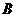 、
、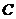 三點的截面和球心的距離是球直徑的
三點的截面和球心的距離是球直徑的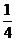 ,且
,且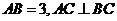 ,
,
則球面的面積為
.
15.設直線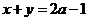 與圓
與圓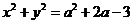 的交點為
的交點為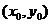 ,當
,當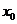 、
、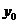 取最小值
取最小值
時,實數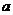 的值為
.
的值為
.
16.給出下面四個命題,其中正確命題的序號是
(填出所有正確命題的序號).
① 若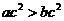 ,則
,則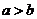 ;
;
② 函數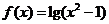 的值域為
的值域為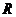 ;
;
③ 數列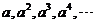 一定為等比數列;
一定為等比數列;
④ 兩個非零向量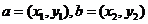 ,若
,若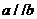 ,則
,則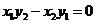 .
.
三、解答題:本大題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
17.(本小題滿分10分)
在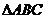 中,
中,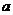 、
、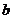 、
、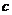 分別是角
分別是角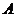 、
、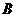 、
、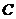 的對邊,且
的對邊,且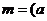 、
、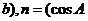 、
、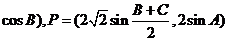 ,若
,若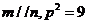 ,試判斷三角形的形狀.
,試判斷三角形的形狀.
18.(本小題滿分12分)
某會議室用5盞燈照明,每盞燈各使用燈泡一只,且型號相同.假定每盞燈能否正常照明只與燈泡的壽命有關,該型號的燈泡壽命為1年以上的概率為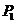 ,壽命為2年以上的概率為
,壽命為2年以上的概率為 ,從使用之日起每滿1年進行一次燈泡更換工作,只更換已壞的燈泡,平時不換.
,從使用之日起每滿1年進行一次燈泡更換工作,只更換已壞的燈泡,平時不換.
(1)在第一次燈泡更換工作中,求不需要更換燈泡的概率和更換2只燈泡的概率;
(2)第二次燈泡更換工作中,對其中的某一盞燈來說,求該盞燈需要更換燈泡的概率;
(3)當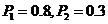 時,求在第二次燈泡更換工作中,至少需要更換4只燈泡的概率(結果保留兩個有效數字)
時,求在第二次燈泡更換工作中,至少需要更換4只燈泡的概率(結果保留兩個有效數字)
19.(本小題滿分12分)
已知函數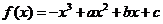 圖象上的點
圖象上的點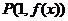 處的切線方程為
處的切線方程為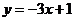 .
.
 (1)若函數
(1)若函數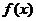 在
在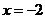 時有極值,求
時有極值,求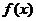 的表達式;
的表達式;
(2)函數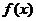 在區間
在區間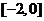 上單調遞增,求實數
上單調遞增,求實數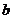 的取值范圍.
的取值范圍.

20.(本小題滿分12分)
如圖所示,已知正四棱柱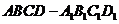 的底面邊長為1,點
的底面邊長為1,點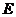 在棱
在棱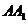 上,
上,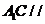 平面
平面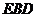 ,截面
,截面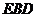 的面積為
的面積為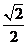 .
.
(1)求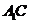 與底面
與底面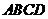 所成角的大小;
所成角的大小;
(2)若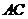 與
與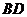 的交點為
的交點為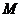 ,點
,點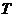 在
在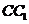 上,且
上,且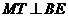 ,求
,求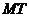 的長.
的長.
21.(本小題滿分12分)
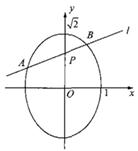 如圖所示,已知橢圓
如圖所示,已知橢圓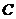 的方程為
的方程為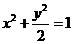 ,點
,點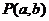 的坐標滿足
的坐標滿足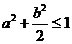 .過點
.過點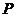 的直線
的直線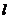 橢圓交于
橢圓交于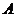 、
、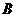 兩點,點
兩點,點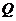 為線段
為線段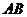 的中點.求:
的中點.求:
(1)點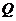 的軌跡方程;
的軌跡方程;
(2)點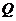 的軌跡與坐標軸的交點的個數.
的軌跡與坐標軸的交點的個數.
22.(本小題滿分12分)
已知數列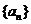 的前
的前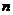 項和
項和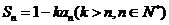 (1)用
(1)用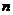 、
、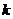 表示
表示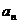 ;
;
(2)數列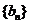 對任意正整數
對任意正整數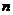 ,均有
,均有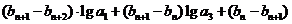

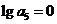 ,求證:數列
,求證:數列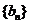 為等差數列;
為等差數列;
(3)在(1)、(2)中,設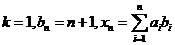 ,求證:
,求證: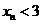 .
.

1.B 2.C 3.B 4.C 5.B 6.B 7.C 8.B 9.C 10.B 
11.C 12.D
【解析】
3.當 時,函數
時,函數 在
在 上,
上, 恒成立即
恒成立即 在
在 上恒成立,可得
上恒成立,可得

當 時,函數
時,函數 在
在 上,
上, 恒成立
恒成立
即 在
在 上恒成立
上恒成立
可得 ,對于任意
,對于任意 恒成立
恒成立
所以 ,綜上得
,綜上得 .
.
4.解法一:聯立 ,得
,得 .
.
 方程總有解,需
方程總有解,需 恒成立
恒成立
即 恒成立,得
恒成立,得 恒成立
恒成立
 ;又
;又

 的取值范圍為
的取值范圍為 .
.
解法二:數形結合,因為直線 恒過定點(0,1),要使直線與橢圓
恒過定點(0,1),要使直線與橢圓 總有交點當日僅當點(0,1)在橢圓上或橢圓內,即
總有交點當日僅當點(0,1)在橢圓上或橢圓內,即

 又
又

 的取值范圍為
的取值范圍為 .
.
5.

7.展開式前三項的系數滿足 可解得
可解得 ,或
,或 (舍去).從而可知有理項為
(舍去).從而可知有理項為 ,故C正確.
,故C正確.
8. ,欲使
,欲使 為奇函數,須使
為奇函數,須使 ,觀察可知,
,觀察可知, 、
、 不符合要求,若
不符合要求,若 ,則
,則
 ,其在
,其在 上是減函數,故B正確
上是減函數,故B正確
當 時,
時, ,其在
,其在 上是增函數,不符合要求.
上是增函數,不符合要求.
9. 等價于
等價于

畫圖可知 ,故
,故 .
.
10.如圖乙所示.設 ,點
,點 到直線
到直線 的距離為
的距離為 ,則由拋物線定義得
,則由拋物線定義得 ,
,

又由點 在橢圓上,及橢圓第一定義得
在橢圓上,及橢圓第一定義得
由橢圓第二定義得 ,解之得
,解之得 .
.
11.從52張牌中任意取13張牌的全部取法為 ;缺少某一種花色的取法為
;缺少某一種花色的取法為 ,缺少兩種花色的取法為
,缺少兩種花色的取法為 ,缺少三種花色的取法為
,缺少三種花色的取法為 ,根據容斥原理可知四種花色齊全的取法為
,根據容斥原理可知四種花色齊全的取法為 .
.
12.設 中點為
中點為 ,連
,連 .由已知得
.由已知得 平面
平面 ,作
,作 ,交
,交 的延長線于點
的延長線于點 ,連
,連 .則
.則 為所求,設
為所求,設 ,則
,則 ,在
,在
中可求出 ,則
,則 .
.
二、填空題
13. .
.
提示:可以用換元法,原不等式為 也可以用數形結合法.
也可以用數形結合法.
令 ,在同一坐標系內分別畫出這兩個函數的圖象,由圖直觀得解集.
,在同一坐標系內分別畫出這兩個函數的圖象,由圖直觀得解集.
14.12 .提示:經判斷,
.提示:經判斷, 為截面團的直徑,再由巳知可求出球的半徑為
為截面團的直徑,再由巳知可求出球的半徑為 .
.
15. .提示:由于
.提示:由于 得
得
解得 ,又
,又

所以,當 時,
時, 取得最小值.
取得最小值.
16.①②④
三、解答題
17.懈:
 ,由正弦定理得,
,由正弦定理得,

 又
又 ,
,
 ,化簡得
,化簡得
 為等邊三角形.
為等邊三角形.
說明;本題是向量和三角相結合的題目,既考查了向量的基本知識,又考查了三角的有關知識,三角形的形狀既可由角確定。也可由邊確定,因此既可從角入手,把邊化為角;也可從邊入手,把角化為邊來判斷三角形的形狀.
18.解:(1)在第一次更換燈泡工作中,不需要更換燈泡的概率為 需要更換2只燈泡的概率為
需要更換2只燈泡的概率為 .
.
(2)對該盞燈來說,在第1、2次都更換了燈泡的概率為 ,在第一次未更換燈泡而在第二次需要更換燈泡的概率為
,在第一次未更換燈泡而在第二次需要更換燈泡的概率為 ,故所求的概率為
,故所求的概率為 .
.
(3)當 時,
時,
由(2)知第二次燈泡更換工作中,某盞燈更換的概率
故至少換4只燈泡的概率為



19.解: ]
]
因為函數 在
在 處的切線斜率為
處的切線斜率為
所以
即 ①
①
又
得 ②
②
(1)函數 在
在 時有極值
時有極值
 ③
③
解式①②③得
所以 .
.
(2)因為函數 在區間
在區間 上單調遞增,所以導函數
上單調遞增,所以導函數 在區間
在區間 的值恒大于或等于零.
的值恒大于或等于零.
則
得 ,所以實數
,所以實數 的取值范圍為
的取值范圍為 .
.
20.解:(1)連接 因為
因為 平面
平面 ,平面
,平面 平面
平面
所以 ;又
;又 為
為 的中點,故
的中點,故 為
為 的中點
的中點

 底面
底面
 為
為 與底面
與底面 所成的角
所成的角
在 中,
中,

 所以
所以 與底面
與底面 所成的角為45°.
所成的角為45°.
(2)解法一;如圖建立直角坐標系
則 ,
, 
 設
設 點的坐標為
點的坐標為
故



 點
點 的坐標為
的坐標為

故 .
.
解法二: 平面
平面
 ,又
,又
 平面
平面
在正方形 中,
中,
 .
.
21.解:(1)設點 、
、 的坐標分別為
的坐標分別為 、
、 ,點
,點 的坐標為
的坐標為
當 時,設直線
時,設直線 的斜率為
的斜率為
 直線
直線 過點
過點
 的方程為
的方程為
又已知 ①
①
 ②
②
 ③
③
 ④
④
∴式①一式②得
 ⑤
⑤
③式+式④得
 ⑥
⑥
∴由式⑤、式⑥及
得點 的坐標滿足方程
的坐標滿足方程
 ⑦
⑦
當 時,
時, 不存在,此時
不存在,此時 平行于
平行于 軸,因此
軸,因此 的中點
的中點 一定落在
一定落在 軸上,即
軸上,即 的坐標為
的坐標為 ,顯然點
,顯然點 (
( ,0)滿足方程⑦
,0)滿足方程⑦
綜上,點 的坐標滿足方程
的坐標滿足方程
設方程⑦所表示的曲線為
則由 ,
,
得
因為 ,又已知
,又已知 ,
,
所以當 時.
時. ,曲線
,曲線 與橢圓
與橢圓 有且只有一個交點
有且只有一個交點 ,
,
當 時,
時, ,曲線
,曲線 與橢圓
與橢圓 沒有交點,因為(0,0)在橢圓內,又在曲線
沒有交點,因為(0,0)在橢圓內,又在曲線 上,所以曲線
上,所以曲線 在橢圓內,故點
在橢圓內,故點 的軌跡方程為
的軌跡方程為

(2)由 解得曲線
解得曲線 與
與 軸交于點(0,0),(0,
軸交于點(0,0),(0, )
)
由 解得曲線
解得曲線 與
與 軸交于點(0,0).(
軸交于點(0,0).( ,0)
,0)
當 ,即點
,即點 為原點時,(
為原點時,( ,0)、(0,
,0)、(0, )與(0.0)重合,曲線
)與(0.0)重合,曲線 與坐標軸只有一個交點(0,0).
與坐標軸只有一個交點(0,0).
當 ,且
,且 ,即點
,即點 不在橢圓
不在橢圓 外且在除去原點的
外且在除去原點的 軸上時,曲線
軸上時,曲線 與坐標軸有兩個交點(0,
與坐標軸有兩個交點(0, )與(0,0),同理,當
)與(0,0),同理,當 且
且 時,曲線與坐標軸有兩個交點(
時,曲線與坐標軸有兩個交點( ,o)、(0,0).
,o)、(0,0).
當 ,且
,且 時,即點
時,即點 不在橢圓
不在橢圓 且不在坐標軸上時,曲線與坐標軸有三個交點(
且不在坐標軸上時,曲線與坐標軸有三個交點( ,0)、(0,
,0)、(0, )與(0,0).
)與(0,0).
22.(1)解: ,又
,又
 是以首項為
是以首項為 ,公比為
,公比為 的等比數列.
的等比數列.
 .
.
(2)證明:設數列 的公比為
的公比為 ,則條件等式可化為:
,則條件等式可化為:
 數列
數列 為等差數列,
為等差數列,
(3)證明:由題意知
 ①
①
式① 得
得
 ②
②
式①-式②得



 .
.
www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com