
如圖,制圖工程師要用兩個同中心的邊長均為4的正方形合成一個八角形圖形.由對稱性,圖中8個三角形都是全等的三角形,設 .
.
(1)試用 表示
表示 的面積;
的面積;
(2)求八角形所覆蓋面積的最大值,并指出此時 的大小.
的大小.
(1)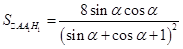 ;(2)
;(2)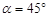 時面積的最大值為
時面積的最大值為 .
.
解析試題分析:(1)要求 的面積,關鍵是求出兩直角邊長,因此我們要把這兩直角邊與正方形的邊長聯系起來,由已知,
的面積,關鍵是求出兩直角邊長,因此我們要把這兩直角邊與正方形的邊長聯系起來,由已知, ,從而直
,從而直 的三邊長之和為正方形的邊長4,所以
的三邊長之和為正方形的邊長4,所以 的邊長可以用
的邊長可以用 表示,也就求出了它的面積;(2)由(1)
表示,也就求出了它的面積;(2)由(1)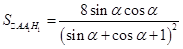 ,要求這個式子的最大值,我們要用換元法變形,這里我們設
,要求這個式子的最大值,我們要用換元法變形,這里我們設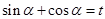 ,則
,則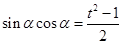 ,于是
,于是 就變為
就變為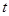 的代數函數
的代數函數 ,不能忘記的是
,不能忘記的是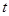 的范圍是
的范圍是 ,
,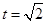 時
時 取最大值.
取最大值.
試題解析:(1)設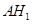 為
為 ,∴
,∴ ,
,  , 3分
, 3分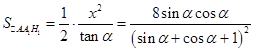 ,
, , 7分
, 7分
(2)令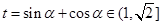 , 9分
, 9分
只需考慮 取到最大值的情況,即為
取到最大值的情況,即為 , 11分
, 11分
當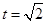 , 即
, 即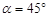 時,
時,  達到最大 13分
達到最大 13分
此時八角形所覆蓋面積的最大值為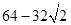 . 14分
. 14分
考點:(1)方程與三角形面積;(2)換元法與三角函數的最大值.


科目:高中數學 來源: 題型:解答題
在△ABC中,內角A,B,C所對的邊分別是a,b,c.已知bsinA=3csinB,a=3,cosB= .
.
(1)求b的值;
(2)求sin(2B- )的值.
)的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在△ABC中,角A,B,C的對邊分別為a,b,c,已知角A= , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a= ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
遼寧廣播電視塔位于沈陽市沈河區青年公園西側,蜿蜒的南運河帶狀公園內,占地8000平方米.全塔分為塔座、塔身、塔樓和桅桿四部分.某數學活動小組在青年公園內的A處測得塔頂B處的仰角為45°. 在水平地面上,沿著A點與塔底中心C處連成的直線行走129米后到達D處(假設可以到達),此時測得塔頂B處的仰角為60°.
(1)請你根據題意,畫出一個ABCD四點間的簡單關系圖形;
(2)根據測量結果,計算遼寧廣播電視塔的高度(精確到1米).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在△ABC中,角A、B、C所對的邊分別為a、b、c,且b2+c2=a2+bc.
(1)求角A的大小;(2)若sinB·sinC=sin2A,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在△ABC中,角A,B,C對應的邊分別是a,b,c.已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com